16.10.2025 — ВСОШ СИРИУС Школьный этап по Математике 4-6 класс: задания и ответы для 3 группы
Авторские решения к этой работе доступны для покупки на нашем сайте:
Группа №3 включает регионы: Астраханская область (49), Курганская область (45), Омская область (55), Оренбургская область (56), Пермский край (59), Республика Башкортостан (02), Самарская область (63), Саратовская область (64), Свердловская область (66), Тюменская область (72), Удмуртская Республика (18), Ульяновская область (73), Ханты-Мансийский автономный округ — Югра (86), Челябинская область (74), Ямало-Ненецкий автономный округ (89).
Рассмотрим задания и ответы по Математике для 4–6 классов:
Навигация
4 класс
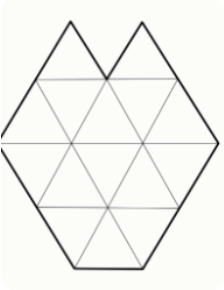
Задание 1. Фигуру, изображённую на рисунке, разрезали на несколько равных по площади частей по линиям сетки (части не обязательно одинаковы). Сколько частей могло получиться? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
Задание 2. Ученики 4 Б класса пошли в кино. В кассе им продали с 3 по 13 места в 4 ряду, места 12 , 13 и 18 в 5 ряду, а остальные ребята сели в 6 ряд на места с 9 по 21. Каждая девочка купила себе по 4 шоколадных батончика, а каждый мальчик по 2 шоколадных батончика и по 2 леденца. Сколько шоколадных батончиков было куплено, если девочек на 5 меньше, чем мальчиков?
Задание 3. Машенька, находясь в комнате, взяла восемь прямоугольных листов цветной бумаги и стала по очереди наклеивать их на окно. На рисунке показано, как выглядит Машина аппликация со стороны комнаты. Какие из этих листов увидит мама, глядя на окно своего дома с улицы?
Задание 4. Варя загадала четырёхзначное число. Известно, что сумма числа тысяч и числа десятков равна 9, сумма числа тысяч и числа сотен на 3 больше, чем сумма числа тысяч и числа десятков, а сумма числа тысяч и числа единиц равна числу десятков. Какое число могла загадать Варя? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
Задание 5. Принц нашёл 4 сундука в заколдованном лесу. В каких‑то двух из них находились алмазы, а в двух других угольки. На каждом сундуке была табличка, и известно, что на сундуках с алмазами написана правда, а на сундуках с угольками ложь. Красный сундук: «Тут лежат алмазы». Зелёный сундук: «Внутри синего сундука лежат угольки». Синий сундук: «Моё содержимое такое же, как и в зелёном сундуке». Чёрный сундук: «Моё содержимое отличается от содержимого красного сундука (если в одном алмазы, то в другом угольки)». Помогите принцу определить, где что находится.
Красный сундук
Зелёный сундук
Синий сундук
Чёрный сундук
Алмазы
Угольки
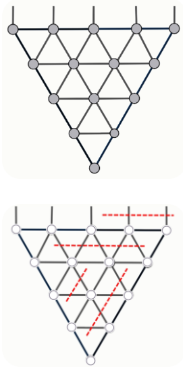
Задание 6. Вася нашёл бабушкино жемчужное ожерелье, которое висело так, как показано на рисунке справа. Он взял ножницы и разрезал часть нитей, как показано на рисунке внизу. Какая жемчужина теперь висит ниже всех?
Задание 7. В системе авиаперевозок всегда указывается местное время взлёта и посадки. Пассажирский самолёт вылетел из города Плюсинск в 17:00 и приземлился в Минусинске в 01:00 следующего дня. Грузовой самолёт летит в два раза медленнее пассажирского. Грузовой самолёт вылетел из Минусинска в 16:00, приземлился в Плюсинске в 11:00 следующего дня, разгрузился и ровно в полночь вылетел обратно в Минусинск. Известно, что грузовой самолёт летит меньше суток. В какое время он прибудет в Минусинск? Ответ запишите в 24 часовом формате ЧЧ:ММ.
Задание 8. Все платья принцессы либо белые, либо розовые, либо бело-розовые. А в гардеробной у неё сущий кавардак! Ведь среди любых 15 платьев найдётся хотя бы одно чисто розовое, а среди любых 11 платьев найдётся хотя бы одно чисто белое. Какое наибольшее количество бело-розовых платьев может быть у принцессы, если всего платьев не менее 18?
5 класс
Задание 1. Декоратор готовит реквизит. У него есть 2025 шариков и три краски: белая, красная и синяя. Он хочет, чтобы каждый шарик был покрашен ровно в два цвета и при этом никакой цвет не встречался в трёх шариках подряд. Первый шарик красно‑синий, второй бело‑синий. В какие цвета окрашен 2025‑й шарик?
Белый и синий
Белый и красный
Красный и синий
→ Получить ответы
Задание 2. У Васи есть два набора карточек: в одном наборе карточки с квадратами чисел от 1 до 9 включительно, а во втором с квадратами чисел от 10 до 20 включительно. Вася может достать взять одну карточку из первого набора и одну — из второго, и составить из этих карточек число. Он хочет, чтобы полученное число было пятизначным и чтобы в нём было не больше двух различных цифр. Какое число может получить Вася? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
→ Получить ответы
Задание 3. Ира решила придумать своё решето Эратосфена для поиска красивых чисел в пределах от 10 до 100. Сначала Ира вычеркнула все числа, в которых одна из цифр делится на другую. Затем Ира вычеркнула все чётные, а потом устала и решила, что все оставшиеся числа красивые. Запишите в ответ сумму самого маленького и самого большого красивых чисел.
→ Получить ответы
Задание 4. Святослав из 5 Я заметил, что, как бы он ни набрал из своего класса команду для игры в бейсбол из 13 человек, в ней обязательно будет мальчик. А среди любых 6 человек будет хотя бы три девочки. Какое наибольшее количество детей могло учиться в 5 Я?
→ Получить ответы
Задание 5. Нильс решил на каникулах изучить Швецию. Он выехал из Гётеборга и половину пути проехал на автобусе. В Стокгольме он собирался пересесть на поезд и проехать на нём вторую половину пути до Эстерсунда, но случайно купил билет не на ту дату его поезд ушёл четыре дня назад. Чтобы родители, которые ждали его в Эстерсунде, не волновались, он вызвал диких гусей, которые летают в два раза быстрее движения поезда. С их помощью Нильс прибыл в Эстерсунд как раз в момент, когда приехал поезд. А сколько дней заняла бы вся дорога, если бы он сразу полетел на гусях?
→ Получить ответы
Задание 6. Школьники в лагере записывались на кружки. На программирование записалось 35 человек, на футбол — 45 , а на рисование 40 . Руководство лагеря составило списки. Оказалось, что детей, записавшихся ровно на один кружок, столько же, сколько тех, кто записался ровно на два кружка, и столько же, сколько тех, кто записался ровно на три кружка. Сколько всего школьников в этом лагере, если каждый ребенок был обязан записаться хотя бы в один кружок?
→ Получить ответы
Задание 7. Тёмный властелин приказал вырастить лабиринт безумия для своих врагов. В лабиринте должен быть один вход и один выход; между любыми двумя местами в лабиринте есть единственный путь, а на дорожках могут встречаться либо перекрёстки с четырьмя вариантами пути (включая тот, по которому пришли), либо тупики. Сколько всего перекрёстков в этом лабиринте, если тупиков 24?
→ Получить ответы
Задание 8. Учитель раздал Антону, Борису, Виктору, Галине и Динаре пять разных прямоугольников с площадью 36 и целыми длинами сторон. Известно, что: девочкам достались фигуры, у которых обе стороны чётные; у Антона и Галины самый большой и самый маленький периметры (но неизвестно, у кого какой); у Виктора сумма длины и ширины является простым числом. Прямоугольники с какими сторонами достались каждому из ребят?
Белый и синий
Белый и красный
Красный и синий
→ Получить ответы
Задание 2. У Васи есть два набора карточек: в одном наборе карточки с квадратами чисел от 1 до 9 включительно, а во втором с квадратами чисел от 10 до 20 включительно. Вася может достать взять одну карточку из первого набора и одну — из второго, и составить из этих карточек число. Он хочет, чтобы полученное число было пятизначным и чтобы в нём было не больше двух различных цифр. Какое число может получить Вася? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
→ Получить ответы
Задание 3. Ира решила придумать своё решето Эратосфена для поиска красивых чисел в пределах от 10 до 100. Сначала Ира вычеркнула все числа, в которых одна из цифр делится на другую. Затем Ира вычеркнула все чётные, а потом устала и решила, что все оставшиеся числа красивые. Запишите в ответ сумму самого маленького и самого большого красивых чисел.
→ Получить ответы
Задание 4. Святослав из 5 Я заметил, что, как бы он ни набрал из своего класса команду для игры в бейсбол из 13 человек, в ней обязательно будет мальчик. А среди любых 6 человек будет хотя бы три девочки. Какое наибольшее количество детей могло учиться в 5 Я?
→ Получить ответы
Задание 5. Нильс решил на каникулах изучить Швецию. Он выехал из Гётеборга и половину пути проехал на автобусе. В Стокгольме он собирался пересесть на поезд и проехать на нём вторую половину пути до Эстерсунда, но случайно купил билет не на ту дату его поезд ушёл четыре дня назад. Чтобы родители, которые ждали его в Эстерсунде, не волновались, он вызвал диких гусей, которые летают в два раза быстрее движения поезда. С их помощью Нильс прибыл в Эстерсунд как раз в момент, когда приехал поезд. А сколько дней заняла бы вся дорога, если бы он сразу полетел на гусях?
→ Получить ответы
Задание 6. Школьники в лагере записывались на кружки. На программирование записалось 35 человек, на футбол — 45 , а на рисование 40 . Руководство лагеря составило списки. Оказалось, что детей, записавшихся ровно на один кружок, столько же, сколько тех, кто записался ровно на два кружка, и столько же, сколько тех, кто записался ровно на три кружка. Сколько всего школьников в этом лагере, если каждый ребенок был обязан записаться хотя бы в один кружок?
→ Получить ответы
Задание 7. Тёмный властелин приказал вырастить лабиринт безумия для своих врагов. В лабиринте должен быть один вход и один выход; между любыми двумя местами в лабиринте есть единственный путь, а на дорожках могут встречаться либо перекрёстки с четырьмя вариантами пути (включая тот, по которому пришли), либо тупики. Сколько всего перекрёстков в этом лабиринте, если тупиков 24?
→ Получить ответы
Задание 8. Учитель раздал Антону, Борису, Виктору, Галине и Динаре пять разных прямоугольников с площадью 36 и целыми длинами сторон. Известно, что: девочкам достались фигуры, у которых обе стороны чётные; у Антона и Галины самый большой и самый маленький периметры (но неизвестно, у кого какой); у Виктора сумма длины и ширины является простым числом. Прямоугольники с какими сторонами достались каждому из ребят?
6 класс
Задание 1. В комнате находятся Игорь, Кирилл, Лев и Макар. Каждый из них либо рыцарь, либо лжец. Рыцари всегда говорят правду, а лжецы всегда лгут. Между ними состоялся следующий разговор. Игорь: «Мы с Макаром относимся к разным типам». Кирилл: «Мы со Львом относимся к одному типу». Игорь: «Кирилл лжец». Сколько среди них рыцарей?
К какому типу относится каждый из них?
Игорь
Кирилл
Лев
Макар
Рыцарь
Лжец
Невозможно определить
Задание 2. Вася взял белый прямоугольник 36×45 и начал его красить: каёмку толщиной в 1 клетку в чёрный цвет, следующую каёмку он оставил белой, затем снова чёрная каёмка и т. д. На рисунке показан аналогичный прямоугольник 5×7 .
Найдите разность количества чёрных и белых клеток в Васином прямоугольнике.

Задание 3. Десять человек, каждый из которых в красном или синем колпаке, встали в колонну. Каждый, кто в красном колпаке, сказал, сколько людей в красных колпаках впереди него. Каждый, кто в синем колпаке, сказал, сколько людей в синих колпаках позади него. Сумма названных чисел оказалась равна 21. Людей в красных колпаках не меньше, чем в синих. Сколько было людей в красных колпаках?
Задание 4. В семье есть папа, мама и несколько детей. 31 января 2022 года сумма их возрастов (включая родителей) равнялась 60 , 31 марта 2023 67 , 31 августа 2025 77 . Новых детей за это время не появилось (и старые никуда не делись). Сколько могло быть детей в семье?
Задание 5. У Андрея есть 15 кубиков (кубики стандартные, на гранях числа от 1 до 6 , значения на противоположных гранях дают в сумме 7). Андрей ставит кубики по следующему правилу: если на верхней грани кубика написана единица, двойка или тройка, то число на нижней грани следующего кубика должно быть вдвое больше, а для чисел от 4 до 6 на нижней грани следующего кубика должно стоять число на 3 меньше. Андрей таким образом построил башню из 15 15 кубиков. Какое число НЕ может быть верхним на 15 м кубике? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
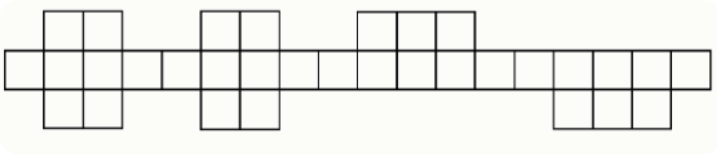
Задание 6. Сколькими способами можно разрезать фигуру на рисунке на части размером по четыре клетки?
Задание 7. У Макса есть несколько талеров. Этих денег хватит, чтобы купить 8 огурцов (и даже ещё останется), но не хватит для покупки шести помидоров. Одиннадцать огурцов стоят столько же, сколько восемь помидоров. Большая тарелка овощей стоимостью 70 талеров также оказалась не по карману Максу. Огурец стоит целое число талеров, и помидор тоже стоит целое число талеров. Сколько талеров у Макса?
Задание 8. В конкурсе середнячков приняли участие 49 танцоров, каждый из которых на жеребьёвке получил уникальный номерок с числом 1 , 2 , 3 , … … , 49 . Затем танцоров случайным образом распределили на группы по семь, расположили номера участников внутри группы в порядке возрастания и из каждой выбрали того, чей номер оказался «средним» в ряду. Среди отобранных семи танцоров по такому же принципу выбрали одного. Какое минимальное число может быть написано на его номерке?
Часть ответов по ВсОШ публикуется бесплатно в нашем Telegram-канале: @shcolaotvet