16.10.2025 — ВСОШ СИРИУС Школьный этап по Математике: задания и ответы для 4-й группы
Авторские решения к этой работе доступны для покупки на нашем сайте:
Группа №4 включает регионы: Алтайский край (22), Амурская область (28), Еврейская автономная область (79), Забайкальский край (75), Иркутская область (38), Камчатский край (41), Кемеровская область — Кузбасс (42), Красноярский край (24), Магаданская область (49), Новосибирская область (54), Приморский край (25), Республика Алтай (04), Республика Бурятия (03), Республика Саха (Якутия) (14), Республика Тыва (17), Республика Хакасия (19), Сахалинская область (65), Томская область (70), Хабаровский край (27), Чукотский автономный округ (87)
Рассмотрим задания и ответы по Математике для 7–11 классов:
Навигация
7 класс
Задание 1. За победу в командных соревнованиях Ане, Боре, Варе, Глебу и Диме вручили мяч и кубок. Аня получила мяч от Глеба, а кубок передала Боре. Дима передал кубок Ане, а мяч получил от Бори. Варя получила мяч от Димы, а кубок от Глеба. Боря получил мяч от Ани, а кубок передал Глебу. Больше никто никому ничего не передавал.
У кого кубок был изначально? У кого мяч был изначально? У кого кубок оказался в конце? У кого мяч оказался в конце?
У Ани
У Бори
У Вари
У Глеба
У Димы
Ответ: Кубок изначально: У Даши Мяч изначально: У Гены Кубок в конце: У Бори Мяч в конце: У Ани
1.2. За победу в командных соревнованиях Косте, Лене, Маше, Насте и Олегу вручили мяч и кубок. Костя получил кубок от Лены, и передал ей мяч. Олег получил мяч от Лены, а кубок передал Насте. Маша получила мяч от Олега, а кубок передала Лене. Настя передала мяч Косте, а кубок — Маше. Больше никто никому ничего не передавал. У кого кубок был изначально? У кого мяч был изначально? У кого кубок оказался в конце? У кого мяч оказался в конце?
1.3. За победу в командных соревнованиях Кате, Лене, Мише, Никите и Оле вручили мяч и кубок. Катя получила кубок от Лены, а мяч передала Никите. Оля получила кубок от Никиты, а мяч передала Кате. Лена получила кубок от Оли, а мяч отдала Мише. Никита отдал мяч Лене, а кубок получил от Миши. Больше никто никому ничего не передавал. У кого кубок был изначально? У кого мяч был изначально? У кого кубок оказался в конце? У кого мяч оказался в конце?
Ответ: 1.миша 2.оля 3.катя 4.миша
1.4. За победу в командных соревнованиях Ане, Боре, Варе, Глебу и Диме вручили мяч и кубок. Аня получила мяч от Глеба, а кубок передала Боре. Дима передал кубок Ане, а мяч получил от Бори. Варя получила мяч от Димы, а кубок — от Глеба. Боря получил мяч от Ани, а кубок передал Глебу. Больше никто никому ничего не передавал. У кого кубок был изначально? У кого мяч был изначально? У кого кубок оказался в конце? У кого мяч оказался в конце?
Задание 2. В классе 70 % девочек и 30 % мальчиков. Известно, что среди учеников класса 40 % девочек и 20 % мальчиков любят играть в шахматы. Найдите долю любителей шахмат в этом классе. Ответ выразите в процентах.
Ответ: 36
2.2. В классе 40 % девочек и 60 % мальчиков. Известно, что среди учеников класса 30 % девочек и 60 % мальчиков любят играть в шахматы. Найдите долю любителей шахмат в этом классе. Ответ выразите в процентах.
2.3. В классе 30 % девочек и 70 % мальчиков. Известно, что среди учеников класса 40 % девочек и 30 % мальчиков любят играть в шахматы. Найдите долю любителей шахмат в этом классе. Ответ выразите в процентах.
Ответ: 48
Задание 3. На плоскости расположены два треугольника и один отрезок. Сколько могло получиться точек пересечения? Выберите все подходящие варианты. Точкой пересечения называется общая точка каких‑либо двух или трёх фигур.
3.2. На плоскости расположены два треугольника и один отрезок. Сколько могло получиться точек пересечения? Выберите все подходящие варианты.
Ответ: 5, 7, 9, 11, 13, 14
Задание 4. На какую цифру оканчивается сумма всех чисел, кратных 3 и принадлежащих отрезку [300; 829] ?
Ответ: 4
4.2. На какую цифру оканчивается сумма всех чисел, кратных 3 и принадлежащих отрезку [300; 772]?
Ответ: 6
4.3. На какую цифру оканчивается сумма всех чисел, кратных 3 и принадлежащих отрезку [600; 947]?
Ответ: 0
4.4. На какую цифру оканчивается сумма всех чисел, кратных 3 и принадлежащих отрезку [300; 643]?
Ответ: 5
Задание 5. На прямой аллее росли вишня, черешня и яблоня. Известно, что расстояние от вишни до яблони в четыре раза больше расстояния от черешни до яблони. В какой‑то момент на вишню села ворона, а на черешню воробей. Оказалось, что вороне до яблони лететь на 60 метров больше, чем воробью. Немного поклевав ягоды, птицы одновременно полетели навстречу друг другу. Сколько метров мог преодолеть воробей к моменту встречи, если его скорость в 1.5 раза меньше, чем скорость вороны? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
5.2. На прямой аллее росли вишня, черешня и яблоня. Известно, что расстояние от вишни до яблони в пять раз больше расстояния от черешни до яблони. В какой-то момент на вишню села ворона, а на черешню — воробей. Оказалось, что вороне до яблони лететь на 20 метров больше, чем воробью. Немного поклевав ягоды, птицы полетели одновременно навстречу друг другу. Сколько метров мог преодолеть воробей к моменту встречи, если его скорость в 1.5 раза меньше, чем скорость вороны? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
5.3. На прямой аллее росли вишня, черешня и яблоня. Известно, что расстояние от вишни до яблони в шесть раз больше расстояния от черешни до яблони. В какой-то момент на вишню села ворона, а на черешню — воробей. Оказалось, что вороне до яблони лететь на 50 метров больше, чем воробью. Немного поклевав ягоды, птицы одновременно полетели навстречу друг другу. Сколько метров мог преодолеть воробей к моменту встречи, если его скорость в 1.5 раза меньше, чем скорость вороны? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
5.4. На прямой аллее росли вишня, черешня и яблоня. Известно, что расстояние от вишни до яблони в три раза больше расстояния от черешни до яблони. В какой-то момент на вишню села ворона, а на черешню — воробей. Оказалось, что вороне до яблони лететь на 80 метров больше, чем воробью. Немного поклевав ягоды, птицы одновременно полетели навстречу друг другу. Сколько метров мог преодолеть воробей к моменту встречи, если его скорость в 1.5 раза меньше, чем скорость вороны? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
Задание 6. Какое наибольшее количество прямоугольников 1×2 ли 2×1 можно выпилить из фигуры, изображённой на рисунке?
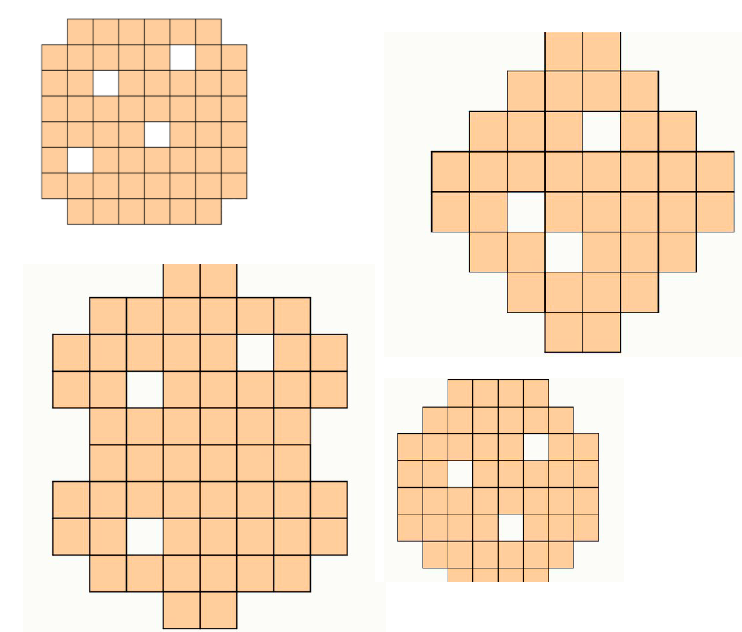
Задание 7. В гостиничном комплексе номера украшены сувенирами трёх видов. Всего разложено 30 фигурок медведей, 25 матрёшек и 20 самоваров. В каждом номере гостиницы обязательно есть хотя бы один сувенир, причём несколько сувениров одного и того же вида в номере быть не может. Ровно в двух номерах есть одновременно самовар и матрёшка, ровно в трёх самовар и медведь, ровно в четырёх медведь и матрёшка. Определите возможное число номеров в гостинице. Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
7.2. В гостиничном комплексе номера украшены сувенирами трёх видов. Всего разложено 30 фигурок медведей, 25 матрёшек и 15 самоваров. В каждом номере гостиницы обязательно есть хотя бы один сувенир, причём несколько сувениров одного и того же вида в номере быть не может. Ровно в двух номерах есть одновременно самовар и матрёшка, ровно в трёх — самовар и медведь, ровно в четырёх — медведь и матрёшка. Определите возможное число номеров в гостинице. Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
7.3. В гостиничном комплексе номера украшены сувенирами трёх видов. Всего разложено 30 фигурок медведей, 25 матрёшек и 15 самоваров. В каждом номере гостиницы обязательно есть хотя бы один сувенир, причём несколько сувениров одного и того же вида в номере быть не может. Ровно в двух номерах есть одновременно самовар и матрёшка, ровно в трёх — самовар и медведь, ровно в четырёх — медведь и матрёшка. Определите возможное число номеров в гостинице. Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
7.4. В гостиничном комплексе номера украшены сувенирами трёх видов. Всего разложено 35 фигурок медведей, 30 матрёшек и 20 самоваров. В каждом номере гостиницы обязательно есть хотя бы один сувенир, причём несколько сувениров одного и того же вида в номере быть не может. Ровно в двух номерах есть одновременно самовар и матрёшка, ровно в трёх — самовар и медведь, ровно в четырёх — медведь и матрёшка. Определите возможное число номеров в гостинице. Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
Задание 8. Сколько существует способов расставить знаки «больше» или «меньше» вместо ∨ ∨ в ребусе К ∨ У ∨ С ∨ О ∨ К так, чтобы он имел решение?
8.2. Сколько существует способов расставить знаки «больше» или «меньше» вместо V в ребусе C V И V P V И V Y V C так, чтобы он имел решение?
8.3. Сколько существует способов расставить знаки «больше» или «меньше» вместо V в ребусе К V У V С V О V К так, чтобы он имел решение?
8.4. Сколько существует способов расставить знаки «больше» или «меньше» вместо V в ребусе C V И V P V И V Y V C так, чтобы он имел решение?
8 класс
Задание 1. На клетчатом поле построили змейку из 100 уголков 5×4(уголок это прямоугольник 5×4, из которого удалили прямоугольник 4×3) толщиной в одну клетку. На рисунке представлен фрагмент змейки, начинающийся с её головы. Каждый уголок, начиная с головы, касается только следующего (и предыдущего) ровно по стороне одной клетки и так до хвоста. Найдите периметр этой змейки. Примечание: на рисунке представлен фрагмент змейки, начинающийся с её головы.
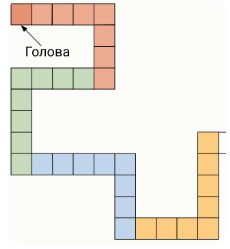
Ответ: 1302
1.2. На клетчатом поле построили змейку из 99 уголков 5 × 3 (уголок — это прямоугольник 5 × 3, из которого удалили прямоугольник 4 × 2) толщиной в одну клетку. На рисунке представлен фрагмент змейки, начинающийся с её головы. Каждый уголок, начиная с головы, касается только следующего (и предыдущего) ровно по стороне одной клетки и так до хвоста. Найдите периметр этой змейки.
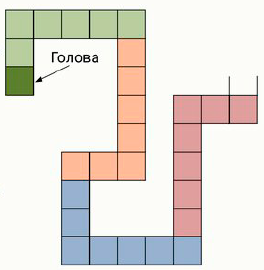
Ответ: 2576
1.3. На клетчатом поле построили змейку из 100 уголков 5 × 4 (уголок — это прямоугольник 5 × 4, из которого удалили прямоугольник 4 × 3) толщиной в одну клетку. На рисунке представлен фрагмент змейки, начинающийся с её головы. Каждый уголок, начиная с головы, касается только следующего (и предыдущего) ровно по стороне одной клетки и так до хвоста. Найдите периметр этой змейки.
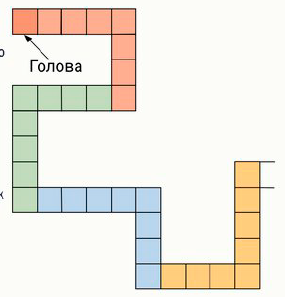
Ответ: 3002
1.4. На клетчатом поле построили змейку из 40 уголков 6 × 4 (уголок — это прямоугольник 6 × 4, из которого удалили прямоугольник 5 × 3) толщиной в одну клетку. На рисунке представлен фрагмент змейки, начинающийся с её головы. Каждый уголок, начиная с головы, касается только следующего (и предыдущего) ровно по стороне одной клетки и так до хвоста. Найдите периметр этой змейки.
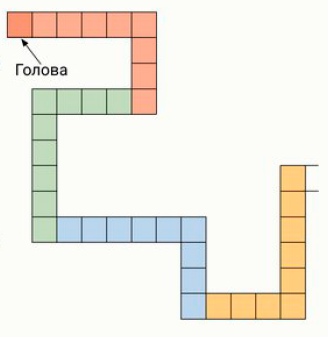
Ответ: 1362
Задание 2. Натуральное число a a разделили на натуральное число b и получили частное c1 и остаток r1. Затем c1 разделили на r1 и получили частное c2 и остаток r2. Разделив c2 на r2 , получили c3=2 и r3=3 При каком наименьшем a a такое возможно?
Ответ: 239
2.2. Натуральное число a разделили на натуральное число b и получили частное c₁ и остаток r₁. Затем c₁ разделили на r₁ и получили частное c₂ и остаток r₂. Разделив c₂ на r₂, получили c₃ = 4 и r₃ = 2.
Ответ: 299
2.3. Натуральное число a разделили на натуральное число b и получили частное c₁ и остаток r₁. Затем c₁ разделили на r₁ и получили частное c₂ и остаток r₂. Разделив c₂ на r₂, получили c₃ = 2 и r₃ = 4. При каком наименьшем a такое возможно?
Ответ: 629
2.4. Натуральное число a разделили на натуральное число b и получили частное c₁ и остаток r₁. Затем c₁ разделили на r₁ и получили частное c₂ и остаток r₂. Разделив c₂ на r₂, получили c₃ = 2 и r₃ = 3. При каком наименьшем a такое возможно?
Ответ: 359
Задание 3. В ряд слева направо стоят несколько человек, каждый из которых — рыцарь или лжец. Рыцари всегда говорят правду, лжецы всегда лгут, в ряду есть и те, и другие. Каждый смотрит либо на начало, либо на конец этого ряда. На просьбу сказать что-то о стоящих перед ним каждый произнёс одну из двух фраз: или «Передо мной хотя бы восемь рыцарей», или «Передо мной хотя бы семь лжецов». Затем все развернулись на 180 и каждый опять сказал одну из тех же самых двух фраз (возможно, ту же самую, а может, другую). Из количества лжецов в ряду вычли количество рыцарей. Найдите наименьшее возможное значение этой разности.
Ответ: 7
3.2. В ряд слева направо стоят несколько человек, каждый из которых — рыцарь или лжец. Рыцари всегда говорят правду, лжецы всегда лгут, в ряду есть и те, и другие. Каждый смотрит либо на начало, либо на конец этого ряда. На просьбу сказать что-то о стоящих перед ним каждый произнёс одну из двух фраз: или «Передо мной хотя бы шесть рыцарей», или «Передо мной хотя бы восемь лжецов». Затем все развернулись на 180° и каждый опять сказал одну из тех же самых двух фраз (возможно, ту же самую, а может, другую). Из количества лжецов в ряду вычли количество рыцарей. Найдите наименьшее возможное значение этой разности.
Ответ: 9
3.3. В ряд слева направо стоят несколько человек, каждый из которых — рыцарь или лжец. Рыцари всегда говорят правду, лжецы всегда лгут, в ряду есть и те, и другие. Каждый смотрит либо на начало, либо на конец этого ряда. На просьбу сказать что-то о стоящих перед ним каждый произнёс одну из двух фраз: или «Передо мной хотя бы восемь рыцарей», или «Передо мной хотя бы семь лжецов». Затем все развернулись на 180° и каждый опять сказал одну из тех же самых двух фраз (возможно, ту же самую, а может, другую). Из количества лжецов в ряду вычли количество рыцарей. Найдите наименьшее возможное значение этой разности.
Ответ: 7
3.4. В ряд слева направо стоят несколько человек, каждый из которых — рыцарь или лжец. Рыцари всегда говорят правду, лжецы всегда лгут, в ряду есть и те, и другие. Каждый смотрит либо на начало, либо на конец этого ряда. На просьбу сказать что-то о стоящих перед ним каждый произнёс одну из двух фраз: или «Передо мной хотя бы семь рыцарей», или «Передо мной хотя бы пять лжецов». Затем все развернулись на 180° и каждый опять сказал одну из тех же самых двух фраз (возможно, ту же самую, а может, другую). Из количества лжецов в ряду вычли количество рыцарей. Найдите наименьшее возможное значение этой разности.
Ответ: 2
Задание 4. Пятнадцать различных натуральных чисел расположены в порядке возрастания. Их сумма равна 1000. Последнее, наибольшее, пятнадцатое, равно 80. Какое наибольшее и какое наименьшее значение может принимать второе число? Наибольшее: Число Наименьшее:
Ответ: 69 и 2
4.2. Пятнадцать различных натуральных чисел расположены в порядке возрастания. Их сумма равна 1000. Последнее, наибольшее, пятнадцатое, равно 80. Какое наибольшее и какое наименьшее значение может принимать второе число?
Ответ: 60 и 2
4.3. Четырнадцать различных натуральных чисел расположены в порядке возрастания. Их сумма равна 800. Последнее, наибольшее, четырнадцатое, равно 70. Какое наибольшее и какое наименьшее значение может принимать второе число?
Ответ: 51 и 2
4.4. Шестнадцать различных натуральных чисел расположены в порядке возрастания. Их сумма равна 1350. Последнее, наибольшее, шестнадцатое, равно 100. Какое наибольшее и какое наименьшее значение может принимать второе число?
Ответ: 40 и 21
Задание 5. В последовательности a1=9, a2=2, a3=13, … каждый член определяется двумя предыдущими:
an+1=an+1an−1.Найдите a60.
5.2. В последовательности a₁ = 8, a₂ = 9, a₃ = 5/4, … каждый член определяется двумя предыдущими:
aₙ₊₁ = (aₙ + 1) / aₙ₋₁. Найдите a₂₀₀.
5.3. В последовательности a₁ = 7, a₂ = 4, a₃ = 5/7, … каждый член определяется двумя предыдущими:
aₙ₊₁ = (aₙ + 1) / aₙ₋₁ Найдите a₁₀₀.
5.4. В последовательности a₁ = 8, a₂ = 9, a₃ = 5/4, … каждый член определяется двумя предыдущими:
aₙ₊₁ = (aₙ + 1) / aₙ₋₁. Найдите a₂₀₀.
Задание 6. В одной школе в математический кружок ходят 14 восьмиклассников и 18 девятиклассников, в другой 12 восьмиклассников и 16 девятиклассников. Всем восьмиклассникам по 14 лет, а всем девятиклассникам по 15. В каждом отделении кружка (каждом классе каждой школы) поровну мальчиков и девочек. Для участия в математическом конкурсе нужно выбрать трёх детей: двух из одной школы, а третьего из другой. Двое детей из одной школы должны быть разного пола и возраста, а третий, из другой школы, должен совпадать с одним в этой паре по возрасту, а с другим по полу. Сколькими способами можно выбрать такую тройку детей?
6.2. В одной школе в математический кружок ходят 12 восьмиклассников и 22 девятиклассника, в другой — 14 восьмиклассников и 20 девятиклассников. Всем восьмиклассникам по 14 лет, а всем девятиклассникам — по 15. В каждом отделении кружка (каждом классе каждой школы) поровну мальчиков и девочек. Для участия в математическом конкурсе нужно выбрать трёх детей: двух из одной школы, а третьего — из другой. Двое детей из одной школы должны быть разного пола и возраста, а третий, из другой школы, должен совпадать с одним в этой паре по возрасту, а с другим — по полу. Сколькими способами можно выбрать такую тройку детей?
6.3. В одной школе в математический кружок ходят 14 восьмиклассников и 12 девятиклассников, в другой — 24 восьмиклассника и 20 девятиклассников. Всем восьмиклассникам по 14 лет, а всем девятиклассникам — по 15. В каждом отделении кружка (каждом классе каждой школы) поровну мальчиков и девочек. Для участия в математическом конкурсе нужно выбрать трёх детей: двух из одной школы, а третьего — из другой. Двое детей из одной школы должны быть разного пола и возраста, а третий, из другой школы, должен совпадать с одним в этой паре по возрасту, а с другим — по полу. Сколькими способами можно выбрать такую тройку детей?
6.4. В одной школе в математический кружок ходят 14 восьмиклассников и 18 девятиклассников, в другой — 12 восьмиклассников и 16 девятиклассников. Всем восьмиклассникам по 14 лет, а всем девятиклассникам — по 15. В каждом отделении кружка (каждом классе каждой школы) поровну мальчиков и девочек. Для участия в математическом конкурсе нужно выбрать трёх детей: двух из одной школы, а третьего — из другой. Двое детей из одной школы должны быть разного пола и возраста, а третий, из другой школы, должен совпадать с одним в этой паре по возрасту, а с другим — по полу. Сколькими способами можно выбрать такую тройку детей?
Задание 7. В равнобедренном треугольнике ABC AB=BC. На стороне BC выбрали точку D, а на стороне AB точку E, так что BD=AE, а DE=BE. Найдите величину угла CEA, если ∠ABC=26∘. Ответ выразите в градусах.
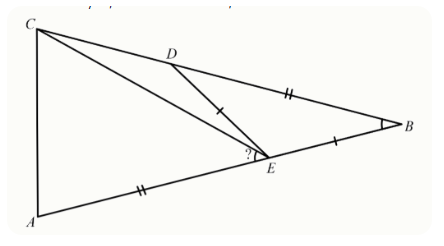
7.2. В равнобедренном треугольнике ABC AB = BC. На стороне BC выбрали точку D, а на стороне AB — точку E, так что BD = AE, а DE = BE. Найдите величину угла CEA, если ∠ABC = 34°. Ответ выразите в градусах.
7.3. В равнобедренном треугольнике ABC AB = BC. На стороне BC выбрали точку D, а на стороне AB — точку E, так что BD = AE, а DE = BE. Найдите величину угла CEA, если ∠ABC = 32°. Ответ выразите в градусах.
Задание 8. Попарно различные натуральные числа a1, a2, a3, a4, b1, b2, b3, b4 таковы, что четыре прямые y=a1x+b1, y=a2x+b2, y=a3x+b3, y=a4x+b4 пересекаются в одной точке. Числа c1, c2, c3, c4 это числа b1, b2 , b3 , b4 , записанные в другом порядке. Оказалось, что прямые y=a1x+c1, y=a2x+c2, y=a3x+c3, y=a4x+c4 тоже пересекаются в одной точке. Найдите минимально возможное значение суммы a1b1+a2b2+a3b3+a4b4.
8.2. Попарно различные натуральные числа a₁, a₂, a₃, a₄, a₅, a₆, b₁, b₂, b₃, b₄, b₅, b₆ таковы, что шесть прямых y = a₁x + b₁, y = a₂x + b₂, y = a₃x + b₃, y = a₄x + b₄, y = a₅x + b₅, y = a₆x + b₆ пересекаются в одной точке. Числа c₁, c₂, c₃, c₄, c₅, c₆ — это числа b₁, b₂, b₃, b₄, b₅, b₆ записанные в другом порядке. Оказалось, что прямые y = a₁x + c₁, y = a₂x + c₂, y = a₃x + c₃, y = a₄x + c₄, y = a₅x + c₅, y = a₆x + c₆ тоже пересекаются в одной точке. Найдите минимально возможное значение суммы a₁b₁ + a₂b₂ + a₃b₃ + a₄b₄ + a₅b₅ + a₆b₆.
8.3. Попарно различные натуральные числа a₁, a₂, a₃, a₄, b₁, b₂, b₃, b₄ таковы, что четыре прямые y = a₁x + b₁, y = a₂x + b₂, y = a₃x + b₃, y = a₄x + b₄ пересекаются в одной точке. Числа c₁, c₂, c₃, c₄ — это числа b₁, b₂, b₃, b₄, записанные в другом порядке. Оказалось, что прямые y = a₁x + c₁, y = a₂x + c₂, y = a₃x + c₃, y = a₄x + c₄ тоже пересекаются в одной точке. Найдите минимально возможное значение суммы a₁b₁ + a₂b₂ + a₃b₃ + a₄b₄.
8.4. Попарно различные натуральные числа a₁, a₂, a₃, b₁, b₂, b₃ таковы, что три прямые y = a₁x + b₁, y = a₂x + b₂, y = a₃x + b₃ пересекаются в одной точке. Числа c₁, c₂, c₃ — это числа b₁, b₂, b₃, записанные в другом порядке. Оказалось, что прямые y = a₁x + c₁, y = a₂x + c₂, y = a₃x + c₃ тоже пересекаются в одной точке. Найдите минимально возможное значение суммы a₁b₁ + a₂b₂ + a₃b₃.
9 класс
Задание 1. На шахматной доске можно выделить различные прямоугольники со сторонами, лежащими на сторонах клеток. Сколько прямоугольников НЕ являются квадратами 5×5?
1.2. На шахматной доске можно выделить различные прямоугольники со сторонами, лежащими на сторонах клеток. Сколько прямоугольников НЕ являются квадратами 6×6?
1.4. На шахматной доске можно выделить различные прямоугольники со сторонами, лежащими на сторонах клеток. Сколько прямоугольников НЕ являются квадратами 4×4?
Задание 2. Сумма двух чисел равна √69, а разность √37. Чему равно их произведение?
2.2 Сумма двух чисел равна √65, а разность √29. Чему равно их произведение?
2.3. Сумма двух чисел равна √75, а разность — √31. Чему равно их произведение?
2.4. Сумма двух чисел равна √77, а разность — √53. Чему равно их произведение?
Задание 3. В остроугольном треугольнике ABC проведена медиана BM, которая делит биссектрису CL в отношении 4:3. Найдите отношение площадей треугольников ABC и ALM.
3.2. В остроугольном треугольнике ABC проведена медиана AD, которая делит высоту BH в отношении 5:3. Найдите отношение площадей треугольников ABC и CDH.
3.3. В остроугольном треугольнике ABC проведена медиана AD, которая делит биссектрису BE в отношении 6:5. Найдите отношение площадей треугольников ABC и CDE.
3.4. В остроугольном треугольнике ABC проведена медиана CN, которая делит высоту AH в отношении 7:5. Найдите отношение площадей треугольников ABC и BNH.
Задание 4. Функция f удовлетворяет условию f(xy)=f(x)+f(y) для всех натуральных чисел x,y . Известно, что f(10)=14 и f(25)=20 . Найдите f(1). Число или дробь Найдите f(2). Число или дробь Найдите f(500).
4.2. Функция f удовлетворяет условию f(xy) = f(x) + f(y) для всех натуральных чисел x, y. Известно, что f(10) = 14 и f(40) = 20. Найдите f(1). Найдите f(2). Найдите f(500).
4.3. Функция f удовлетворяет условию f(x + y) = f(x)f(y) для всех неотрицательных чисел x, y. Известно, что f(20) = 25. Найдите f(0). Найдите f(10). Найдите f(50).
4.4. Функция f удовлетворяет условию f(xy)=f(x)+f(y) для всех натуральных чисел x,y . Известно, что f(10)=14 и f(25)=26 . Найдите f(1). Число или дробь Найдите f(2). Число или дробь Найдите f(400).
4.5. Функция f удовлетворяет условию f(x + y) = f(x)f(y) для всех неотрицательных чисел x, y. Известно, что f(25) = 32. Найдите f(0). Найдите f(5). Найдите f(60).
Задание 5. Параболу, являющуюся графиком функции y = 2x², отразили относительно прямой, описанной уравнением y = x + 3. Определите коэффициенты в уравнении получившейся параболы x = ay² + by + c.
5.2. График функции y = 5x² отразили относительно прямой, описанной уравнением y = 1 — x. Определите коэффициенты в уравнении получившейся параболы x = ay² + by + c.
5.3. Параболу, являющуюся графиком функции y = 4x², отразили относительно прямой, описанной уравнением y = x + 1. Определите коэффициенты в уравнении получившейся параболы x = ay² + by + c.
5.4. График функции y = 3x² отразили относительно прямой, описанной уравнением y = 2 — x. Определите коэффициенты в уравнении получившейся параболы x = ay² + by + c.
Задание 6. Андрей выкладывает картонные квадраты 3 × 3 вдоль диагонали квадрата 4 × 4 следующим образом: сначала по одному квадрату прикладывает к двум противоположным углам, а остальные равномерно выкладывает вдоль диагонали между первыми двумя (то есть центры квадратов делят отрезок между центрами крайних квадратов на равные отрезки). На рисунке показан пример для четырёх квадратов, которые покрывают область площади 44/3.
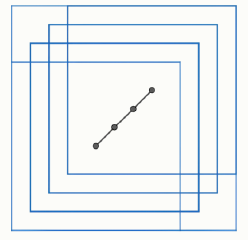
Сколько необходимо квадратов, чтобы они покрыли площадь, равную 314/21? Чему равно минимальное количество квадратов, необходимое для того, чтобы покрыть площадь хотя бы √224?
6.3. Егор выкладывает картонные квадраты 3 × 3 вдоль диагонали квадрата 4 × 4 следующим образом: сначала по одному квадрату прикладывает к двум противоположным углам, а остальные равномерно выкладывает вдоль диагонали между первыми двумя (то есть центры квадратов делят отрезок между центрами крайних квадратов на равные отрезки). На рисунке показан пример для четырёх квадратов, которые покрывают область площади 44/3.
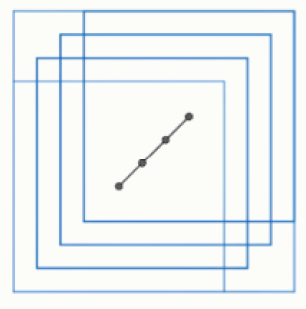
Сколько необходимо квадратов, чтобы они покрыли площадь, равную 254/17? Чему равно минимальное количество квадратов, необходимое для того, чтобы покрыть площадь хотя бы √223?
6.4. Саша выкладывает картонные квадраты 2 × 2 вдоль диагонали квадрата 3 × 3 следующим образом: сначала по одному квадрату прикладывает к двум противоположным углам, а остальные равномерно выкладывает вдоль диагонали между первыми двумя (то есть центры квадратов делят отрезок между центрами крайних квадратов на равные отрезки). На рисунке показан пример для четырёх квадратов, которые покрывают область площади 23/3.
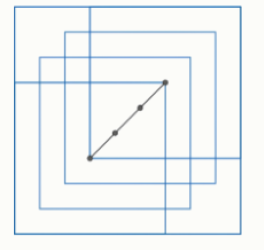
Сколько необходимо квадратов, чтобы они покрыли площадь, равную 335/42? Чему равно минимальное количество квадратов, необходимое для того, чтобы покрыть площадь хотя бы √63?
6.5. Демьян выкладывает картонные квадраты 2×2 вдоль диагонали квадрата 3×3 следующим образом: сначала по одному квадрату прикладывает к двум противоположным углам, а остальные равномерно выкладывает вдоль диагонали между первыми двумя (то есть центры квадратов делят отрезок между центрами крайних квадратов на равные отрезки). На рисунке показан пример для четырёх квадратов, которые покрывают область площади 23/3 .
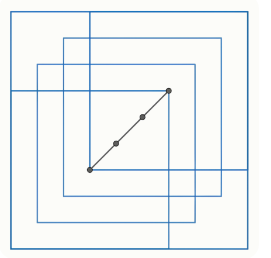
Сколько необходимо квадратов, чтобы они покрыли площадь, равную 255/32? Число Чему равно минимальное количество квадратов, необходимое для того, чтобы покрыть площадь хотя бы 62√?
Задание 7. У Васи есть 35 картонных квадратов 1 × 1, стороны каждого покрашены в красный, жёлтый, зелёный и синий цвета; для всех квадратов эти стороны расположены одинаково относительно друг друга. Вася хочет из них сложить доску 5 × 7. Квадраты можно поворачивать и переворачивать, но соединять допустимо только по сторонам одного цвета. Доски, отличающиеся поворотом или переворотом, считаются разными. Сколько всего различных досок может собрать Вася?
7.2. У Васи есть 30 картонных квадратов 1 × 1, стороны каждого покрашены в красный, жёлтый, зелёный и синий цвета; для всех квадратов эти стороны расположены одинаково относительно друг друга. Вася хочет из них сложить доску 5 × 6. Квадраты можно поворачивать и переворачивать, но соединять допустимо только по сторонам одного цвета. Доски, отличающиеся переворотом, считаются разными. Сколько всего различных досок может собрать Вася?
7.3. У Васи есть 20 картонных квадратов 1 × 1, стороны каждого покрашены в красный, жёлтый, зелёный и синий цвета; для всех квадратов эти стороны расположены одинаково относительно друг друга. Вася хочет из них сложить доску 4 × 5. Квадраты можно поворачивать и переворачивать, но соединять допустимо только по сторонам одного цвета. Доски, отличающиеся поворотом или переворотом, считаются разными. Сколько всего различных досок может собрать Вася?
7.4. У Васи есть 30 картонных квадратов 1 × 1, стороны каждого покрашены в красный, жёлтый, зелёный и синий цвета; для всех квадратов эти стороны расположены одинаково относительно друг друга. Вася хочет из них сложить доску 5 × 6. Квадраты можно поворачивать и переворачивать, но соединять допустимо только по сторонам одного цвета. Доски, отличающиеся переворотом, считаются разными. Сколько всего различных досок может собрать Вася?
7.5. У Васи есть 24 картонных квадрата 1 × 1, стороны каждого покрашены в красный, жёлтый, зелёный и синий цвета; для всех квадратов эти стороны расположены одинаково относительно друг друга. Вася хочет из них сложить доску 4 × 6. Квадраты можно поворачивать и переворачивать, но соединять допустимо только по сторонам одного цвета. Доски, отличающиеся поворотом или переворотом, считаются разными. Сколько всего различных досок может собрать Вася?
Задание 8. У натуральных чисел m, n наибольший общий делитель — НОД(m, n) — равен 11. Найдите все возможные значения НОД(m² — 2mn + n², m² + 9mn + n²). Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
8.2. У натуральных чисел m, n наибольший общий делитель — НОД(m, n) — равен 11. Найдите все возможные значения НОД(m² — 2mn + n², m² + 9mn + n²). Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
8.3. У натуральных чисел a, b наибольший общий делитель — НОД(a, b) — равен 7. Найдите все возможные значения НОД(a² — 2ab + b², a² + 5ab + b²). Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
8.4. У натуральных чисел a, b наибольший общий делитель — НОД(a, b) — равен 3. Найдите все возможные значения НОД(a² + ab + b², a² + 4ab + b²). Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
8.5. У натуральных чисел p, q наибольший общий делитель — НОД(p, q) — равен 5. Найдите все возможные значения НОД(p² + 2pq + q², p² + 7pq + q²). Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
10 класс
11 класс
Часть ответов по ВсОШ публикуется бесплатно в нашем Telegram-канале: @shcolaotvet