Школьный этап ВсОШ СИРИУС по Информатике (ИИ) 5-11 класс, Группа 4 (21.10.2025)

Задание 1. У Кости на рабочем столе десять объектов. Каждый из этих объектов либо файл, либо папка. В каждой из таких папок содержится по пять файлов. Известно, что у Кости ровно 42 файла (в таких папках и на рабочем столе). Сколько папок у Кости на рабочем столе?

Ответ: 8

Задание 2. Есть изначально белый квадрат 8×8. Рассмотрим следующий алгоритм закрашивания его клеток в чёрный цвет. На первом шаге закрашивается произвольная клетка. На каждом следующем шаге закрашивается одна из тех клеток, которые граничат по стороне с закрашенной на предыдущем шаге клеткой. Если таких клеток нет, процесс закрашивания завершается. Какое наименьшее число клеток может быть закрашено данным алгоритмом?

→ Получить все ответы

Задание 3. Рассмотрим строку из 70 символов. Пусть среди первых 40 символов в этой строке ровно m различных. Модель ИИ по величине m делает предсказание (выдаёт целое число, зависящее лишь от m) о количестве различных символов во всей строке. Будем называть ошибкой отличие между ответом модели и верным ответом. При каком наименьшем N существует модель, ошибка которой не превосходит N для любой исходной строки?

→ Получить все ответы

Задание 4. Учитель решил проверить тест автоматически. Предполагалось, что оценка «Сдано» выставляется, если не менее 50 % заданий выполнено верно. Однако проверяющая программа была написана с ошибкой. Она проверяет задания по одному, и если после проверки очередного задания среди проверенных заданий оказывается менее 50 % выполненных верно, то программа выставляет оценку «Не сдано» и заканчивает проверку. Всего в тесте было 20 вопросов. Вася получил оценку «Сдано», Петя получил оценку «Не сдано», при этом Петя дал на N правильных ответов больше, чем Вася. Найдите наибольшее возможное значение N .

→ Получить все ответы

Задание 5. Четыре модели искусственного интеллекта соревновались в решении задач международной олимпиады по математике. Эта олимпиада состоит из шести задач, каждая задача оценивается целым числом баллов от 0 до 7. Награждение медалями и грамотами в зависимости от результатов происходило по следующему принципу:

• золотая медаль — не менее 35 баллов;
• серебряная медаль — не менее 28 баллов и не более 34 баллов
• бронзовая медаль — не менее 19 баллов и не более 27 баллов;
• похвальная грамота — не более 18 баллов, но за хотя бы одну задачу 7 баллов.

Первой модели была присуждена золотая медаль, второй серебряная медаль, третьей бронзовая медаль, четвёртой похвальная грамота. Известно, что первая и четвёртая модели в сумме набрали на 19 баллов меньше, чем вторая и третья. Сколько баллов могли набрать все четыре модели в сумме? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости. Если описанная в условии ситуация невозможна, в ответ запишите 0.

→ Получить все ответы

Задание 6. Стозначное число записывается цифрами 1 и 2 . Модель ИИ по запросу «Верно ли, что пар стоящих рядом единиц столько же, сколько и пар рядом стоящих двоек» выдаёт ответ ДА, если единиц ровно 50, и ответ НЕТ в противном случае. Найдите наименьшее стозначное число, для которого модель выдаёт неверный ответ. В ответ запишите сумму 10 его последних цифр.

Задание 1. Месяц подписки на платную версию искусственного интеллекта стоит 200 рублей, три месяца подписки обойдутся в 500 рублей, а полгода в 900 рублей. На какое наибольшее число месяцев можно купить подписку за 2000 рублей?

→ Получить все ответы

Задание 2. Модель ИИ отвечает на запрос «Является ли число N простым» следующим образом: если число N делится на некоторое натуральное число, большее 1 и меньшее 90 , или N=1, выдаётся ответ «нет». В противном случае выдаётся ответ «да». Найдите наименьшее натуральное число N, большее 90, для которого модель отвечает на запрос неправильно.

→ Получить все ответы

Задание 3. Рассмотрим строку из 80 букв А и Б. Назовём её характеристикой пару чисел ( a , b), где a количество букв А среди первых 50 букв строки, b количество букв А среди последних 50 букв строки. Модель ИИ по характеристике строки выдаёт предсказание (целое число, зависящее лишь от характеристики) о количестве букв А во всей строке. Назовём ошибкой отличие между ответом модели и истинным количеством букв А в строке. При каком наименьшем значении N существует модель, ошибка которой не превосходит N?

→ Получить все ответы

Задание 4. Сто деталей сложены на столе в форме решётки 10×10. Будем говорить, что две детали лежат рядом, если они соседствуют по вертикали, горизонтали или диагонали. Например, угловая деталь лежит рядом с тремя другими деталями. Манипулятор перекладывает эти детали в короб. В его программе заложен следующий алгоритм: если есть две детали, расположенные рядом, нужно переложить какие‑то две детали в короб (манипулятор перекладывает их одновременно). Если таких двух деталей нет, переложить в короб произвольную из оставшихся деталей. Какое наибольшее число операций по перекладыванию деталей может потребоваться данному манипулятору?

→ Получить все ответы

Задание 5. Дан обучающий текст s строка из букв a, b, c. Для каждой буквы x∈ { a , b ,c } договоримся выбирать «следующую букву» так: посмотрим на все места в строке s, где встречается x; если после x стоит какая‑то буква (то есть x не последняя в строке), учтём именно эту следующую букву. Та, которая встречается сразу после x чаще других, и считается «следующей» для x. Если несколько букв равны по частоте, берём ту, что идёт раньше по алфавиту (a<b<c) . Если после x ни разу не стояла никакая буква, «следующей» для x x считаем знак вопроса «?». Если на каком‑то шаге получился «?», то все последующие символы тоже будут «?». Строка: s=abacbcbbccabbc Стартовая буква: a a . Запишите строку из 10 символов: x1x2… x10 , где x1=a, а для каждого k≥1 символ xk+1 это «следующая» для xk по правилу выше.

Задание 1. Чат‑бот программа, которая читает текст и пишет ответы, за один раз может обработать не более 128000 условных единиц текста. Примем, что одно слово это одна условная единица. В уже начатой беседе хранится история объёмом 500 слов. Вы хотите загрузить документ, на каждой странице которого ровно по 400 слов. Ответ системы должен быть равен по длине исходному тексту; промежуточные рассуждения составляют 15% от длины исходного текста. Документ какого максимального объёма можно обработать так, чтобы общая сумма (история +исходный текст + рассуждения + ответ) условных единиц не превысила 128000? Ответ выразите в страницах.

→ Получить все ответы

Задание 2. Смартфон в автоматическом режиме камеры оценивает каждое изображение по двум параметрам x и y выставляя целочисленные баллы от 1 до 6. Считается, что все 36 комбинаций ( x , y) встречаются одинаково часто (как при броске двух игральных кубиков: каждая комбинация граней равновозможна). Камера размывает фон, если x+y⩾7. Петя, не зная y, пользуется упрощённым правилом: он смотрит только на x и говорит «размытие будет» тогда и только тогда, когда x⩾4. С какой вероятностью ответ Пети совпадёт с решением смартфона для случайно выбранной фотографии?

→ Получить все ответы

Задание 3. В обучении программ по примерам (это называют машинным обучением) бывает ошибка: в примерах для тренировки случайно оказываются правильные ответы. Тогда программа не учится рассуждать, а просто запоминает ответы и проваливается на новых задачах. Аналогичная ситуация и у школьников: можно честно разбираться в теме, а можно списывать из «готовых домашних заданий» (ГДЗ). Списывая, легко получать высокие оценки, но знаний мало, и на контрольной это скажется. У школьника 10 домашних заданий и одна контрольная. Для каждого домашнего задания он выбирает: решить самостоятельно (Ч) или списать из ГДЗ (Г). Пусть Kt уровень знаний перед t‑м домашним заданием ( t = 1 , …, 10). Если ученик сам решает задание t , то его уровень знаний повышается на один, иначе уровень знаний не повышается, K1=0 . Оценка за t-е домашнее задание считается так: если решено честно, то Ht=1.5+0.3Kt ; если домашнее задание списано, то Ht=4.5. Оценка за контрольную работу зависит только от знаний после последнего домашнего задания K11:

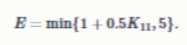
Итоговый средний балл: 40% за домашние, 60% за контрольную:

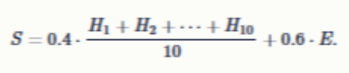
Найдите максимальное значение SS. Ответ округлите до тысячных.

Найдите оптимальное число честно выполненных домашних заданий, при котором SS максимально.

→ Получить все ответы

Задание 4. Учитель объясняет детям, что если они хотят проверить гипотезу, её нужно пытаться опровергнуть. Он загадал правило, которому удовлетворяет тройка целых чисел 1, 2, 4. Известно, что это правило одно из четырёх:

числа строго возрастают;

все числа положительные;

подходят любые три числа;

произведение первого и последнего чисел равно квадрату второго.

Выберите две тройки чисел так, чтобы по паре ответов «да/нет» можно было однозначно понять, какое именно из четырёх правил загадано:

→ Получить все ответы

Задание 5. В задаче бинарной классификации (разделения объектов на 2 класса) дано всего N=800 объектов, из них положительных P=200 и отрицательных N−P=600. Пусть:

• TP — верно предсказанные положительные объекты (True Positives);
• FP — отрицательные объекты, ошибочно предсказанные как положительные (False Positives);
• FN — положительные объекты, ошибочно предсказанные как отрицательные (False Negatives);
• TN — верно предсказанные отрицательные объекты (True Negatives).

Метрики:

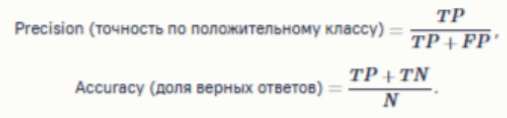
Известно, что Precision =0.5

Найдите диапазон возможных значений Accuracy.

→ Получить все ответы

Задание 6. Данные для выполнения этого задания находятся в файле электронной таблицы. Вы можете скачать файл в одном из трёх форматов: XLSX, ODS, CSV. В документе каждая строка содержит два числа: вероятность положительного исхода pp (число от 0 до 1) и правильную отметку y (0 отрицательный исход, 1 положительный исход). Зададим простое правило предсказания: если p ⩾ 0.6, считаем предсказание равным 1, иначе 0. Найдите количество строк, для которых предсказание совпадает с правильной отметкой y.