15.10.2025 — ВСОШ СИРИУС Школьный этап по Математике 7-11 класс: задания и ответы для 1 группы
Авторские решения к этой работе доступны для покупки на нашем сайте:
Группа №1 включает регионы: Республика Адыгея (01), Республика Дагестан (05), Кабардино-Балкарская Республика (07), Республика Калмыкия (08), Карачаево-Черкесская Республика (09), Республика Коми (11), Чеченская Республика (20), Краснодарский край (23, 93, 123), Ставропольский край (26), Архангельская область (29), Волгоградская область (34), Вологодская область (35), Мурманская область (51), Новгородская область (53), Псковская область (60), Ростовская область (61), Донецкая Народная Республика (80), Луганская Народная Республика (81), Республика Крым (82), Херсонская область (85), город Севастополь (92) и Запорожская область (92).
Рассмотрим задания и ответы по Математике для 7–11 классов:
Навигация
7 класс
Задание 1. Если от трёхзначного числа отнять 5, оно разделится на 5; если отнять 8, оно разделится на 8; если отнять 13 оно разделится на 13 . Найдите это число.
Ответ: 503
Задание 1.1 Если от трёхзначного числа отнять 6, оно разделится на 6; если отнять 7, оно разделится на 7; если отнять 13 — оно разделится на 13. Найдите это число.
→ Получить ответы
Задание 1.2 Если от трёхзначного числа отнять 7, оно разделится на 7; если отнять 9, оно разделится на 9; если отнять 11 — оно разделится на 11. Найдите это число.
Ответ: 546
Задание 1.3 Если от трёхзначного числа отнять 5, оно разделится на 5; если отнять 8, оно разделится на 8; если отнять 13 — оно разделится на 13. Найдите это число.
→ Получить ответы
Задание 2. Из куска проволоки согнули прямоугольник, длина которого в 4 раза больше ширины. Затем разогнули проволоку и согнули из неё другой прямоугольник с длиной на 10 % больше, чем раньше. На сколько процентов уменьшилась его ширина?
Ответ: 60%
Задание 2.1 Из куска проволоки согнули прямоугольник, длина которого в 3 раза больше ширины. Затем разогнули проволоку и согнули из неё другой прямоугольник с длиной на 20% больше, чем раньше. На сколько процентов уменьшилась его ширина?
→ Получить ответы
Задание 2.2 Из куска проволоки согнули прямоугольник, длина которого в 5 раза больше ширины. Затем разогнули проволоку и согнули из неё другой прямоугольник с длиной на 16 % больше, чем раньше. На сколько процентов уменьшилась его ширина?
Ответ: 20%
Задание 2.3 Из куска проволоки согнули прямоугольник, длина которого в 2 раза больше ширины. Затем разогнули проволоку и согнули из неё другой прямоугольник с длиной на 10 % больше, чем раньше. На сколько процентов уменьшилась его ширина?
→ Получить ответы
Задание 3. В каждой клетке квадрата 18×18 лежит монета орлом вверх. Какое наименьшее количество монет нужно перевернуть, чтобы в результате на каждой горизонтали, вертикали и обеих диагоналях были как монеты, лежащие вверх орлом, так и монеты, лежащие вверх решкой?
Ответ: 72
Задание 3.1 В каждой клетке квадрата 12 х 12 лежит монета орлом вверх. Какое наименьшее количество монет нужно перевернуть, чтобы в результате на каждой горизонтали, вертикали и обеих диагоналях были как монеты, лежащие вверх орлом, так и монеты, лежащие вверх решкой?
→ Получить ответы
Задание 3.2 В каждой клетке квадрата 16 х 16 лежит монета орлом вверх. Какое наименьшее количество монет нужно перевернуть, чтобы в результате на каждой горизонтали, вертикали и обеих диагоналях были как монеты, лежащие вверх орлом, так и монеты, лежащие вверх решкой?
Ответ: 162
Задание 3.3 В каждой клетке квадрата 14 х 14 лежит монета орлом вверх. Какое наименьшее количество монет нужно перевернуть, чтобы в результате на каждой горизонтали, вертикали и обеих диагоналях были как монеты, лежащие вверх орлом, так и монеты, лежащие вверх решкой?
→ Получить ответы
Задание 4. В одной из двух канистр содержится 18 литров воды, другая пуста. Из первой канистры во вторую переливают половину имеющейся там воды, затем из второй в первую треть имеющейся там воды, потом из первой во вторую четверть имеющейся там воды и т. д. Сколько воды будет в первой канистре после 997 переливаний? Ответ выразите в литрах.
Ответ: 7 литров
Задание 4.1 В одной из двух канистр содержится 14 литров воды, другая пуста. Из первой канистры вторую переливают половину имеющейся там воды, затем из второй в первую — треть имеющейся там воды, потом из первой во вторую — четверть имеющейся там воды и т. д. Сколько воды будет в первой канистре после 1003 переливаний? Ответ выразите в литрах.
→ Получить ответы
Задание 4.2 В одной из двух канистр содержится 10 литров воды, другая пуста. Из первой канистры во вторую переливают половину имеющейся там воды, затем из второй в первую — треть имеющейся там воды, потом из первой во вторую — четверть имеющейся там воды и т. д. Сколько воды будет в первой канистре после 1001 переливания? Ответ выразите в литрах.
Ответ: 5 литров
Задание 4.3 В одной из двух канистр содержится 20 литров воды, другая пуста. Из первой канистры во вторую переливают половину имеющейся там воды, затем из второй в первую — треть имеющейся там воды, потом из первой во вторую — четверть имеющейся там воды и т. д. Сколько воды будет в первой канистре после 999 переливаний? Ответ выразите в литрах.
→ Получить ответы
Задание 5. Стороны клетчатого многоугольника с периметром 20 , проходят по линиям сетки? Сторона клетки равна 1. Определите минимально возможное количество его вершин.
Определите максимально возможное количество его вершин.
→ Получить ответы
Задание 5.1 Стороны клетчатого многоугольника с периметром 28 , проходят по линиям сетки? Сторона клетки равна 1. Определите минимально возможное количество его вершин.
Определите максимально возможное количество его вершин.
→ Получить ответы
Задание 5.2 Стороны клетчатого многоугольника с периметром 24 , проходят по линиям сетки? Сторона клетки равна 1. Определите минимально возможное количество его вершин.
Определите максимально возможное количество его вершин.
→ Получить ответы
Задание 5.3 Стороны клетчатого многоугольника с периметром 16 , проходят по линиям сетки? Сторона клетки равна 1. Определите минимально возможное количество его вершин.
Определите максимально возможное количество его вершин.
→ Получить ответы
Задание 6. Все числа от 1 до 800 выписали подряд: 123456789101112 … 799800 . Сколько раз в этом ряду сразу после цифры 5 стоит цифра 6?
→ Получить ответы
Задание 6.1 Все числа от 1 до 500 выписали подряд: 123456789101112 … 499500. Сколько раз в этом ряду сразу после цифры 2 стоит цифра 3?
→ Получить ответы
Задание 6.2 Все числа от 1 до 700 выписали подряд: 123456789101112 … 699700. Сколько раз в этом ряду сразу после цифры 4 стоит цифра 5?
→ Получить ответы
Задание 6.3 Все числа от 1 до 600 выписали подряд: 123456789101112 … 599600. Сколько раз в этом ряду сразу после цифры 3 стоит цифра 4?
→ Получить ответы
Задание 7. В клетках таблицы 2×2 записаны положительные числа. Саша и Паша выбрали клетку и заштриховали её серым. Саша посчитал сумму чисел в строке, в которой она находится, а Паша проделал ту же самую операцию для столбца. Потом мальчики перемножили свои суммы и получили результат, в 3 раза больший числа в заштрихованной клетке. Оказалось, что это условие справедливо для любой из четырёх клеток. Найдите сумму всех чисел в таблице.
→ Получить ответы
Задание 7.1 B клетках таблицы 2 х 2 записаны положительные числа. Витя и Женя выбрали клетку и заштриховали её серым. Витя посчитал сумму чисел в строке, в которой она находится, Женя проделал ту же самую операцию для столбца. Потом мальчики перемножили свои суммы и получили результат, в 4 раза меньший числа в заштрихованной клетке. Оказалось, что это условие справедливо для любой из четырёх клеток. Найдите сумму всех чисел в таблице.
→ Получить ответы
Задание 7.2 B клетках таблицы 2 х 2 записаны положительные числа. Петя и Вася выбрали клетку и заштриховали её серым. Петя посчитал сумму чисел в строке, в которой она находится, Вася проделал ту же самую операцию для столбца. Потом мальчики перемножили свои суммы и получили результат, в 2 раза меньший числа в заштрихованной клетке. Оказалось, что это условие справедливо для любой из четырёх клеток. Найдите сумму всех чисел в таблице.
→ Получить ответы
Задание 7.3 B клетках таблицы 2 х 2 записаны положительные числа. Толя и Рома выбрали клетку и заштриховали её серым. Толя посчитал сумму чисел в строке, в которой она находится, Рома проделал ту же самую операцию для столбца. Потом мальчики перемножили свои суммы и получили результат, в 5 раз больший числа в заштрихованной клетке. Оказалось, что это условие справедливо для любой из четырёх клеток. Найдите сумму всех чисел в таблице.
→ Получить ответы
Задание 8. По контуру квадрата в одном направлении ползут три жука, скорости которых постоянны и различны. Найдите скорость самого медленного из жуков, если скорости других равны 20 мм/с и 60 мм/с, а все обгоны происходят только в вершинах квадрата. Ответ выразите в мм/с.
→ Получить ответы
Задание 8.1 По контуру квадрата в одном направлении ползут три жука, скорости которых постоянны и различны. Найдите скорость самого медленного из жуков, если скорости других равны 10 мм/с и 30 мм/с, а все обгоны происходят только в вершинах квадрата. Ответ выразите в мм/с.
→ Получить ответы
Задание 8.2 По контуру квадрата в одном направлении ползут три жука, скорости которых постоянны и различны. Найдите скорость самого медленного из жуков, если скорости других равны 15 мм/с и 45 мм/с, а все обгоны происходят только в вершинах квадрата. Ответ выразите в мм/с.
→ Получить ответы
Задание 8.3 По контуру квадрата в одном направлении ползут три жука, скорости которых постоянны и различны. Найдите скорость самого медленного из жуков, если скорости других равны 25 мм/с и 75 мм/с, а все обгоны происходят только в вершинах квадрата. Ответ выразите B мм/с.
Ответ: 503
Задание 1.1 Если от трёхзначного числа отнять 6, оно разделится на 6; если отнять 7, оно разделится на 7; если отнять 13 — оно разделится на 13. Найдите это число.
→ Получить ответы
Задание 1.2 Если от трёхзначного числа отнять 7, оно разделится на 7; если отнять 9, оно разделится на 9; если отнять 11 — оно разделится на 11. Найдите это число.
Ответ: 546
Задание 1.3 Если от трёхзначного числа отнять 5, оно разделится на 5; если отнять 8, оно разделится на 8; если отнять 13 — оно разделится на 13. Найдите это число.
→ Получить ответы
Задание 2. Из куска проволоки согнули прямоугольник, длина которого в 4 раза больше ширины. Затем разогнули проволоку и согнули из неё другой прямоугольник с длиной на 10 % больше, чем раньше. На сколько процентов уменьшилась его ширина?
Ответ: 60%
Задание 2.1 Из куска проволоки согнули прямоугольник, длина которого в 3 раза больше ширины. Затем разогнули проволоку и согнули из неё другой прямоугольник с длиной на 20% больше, чем раньше. На сколько процентов уменьшилась его ширина?
→ Получить ответы
Задание 2.2 Из куска проволоки согнули прямоугольник, длина которого в 5 раза больше ширины. Затем разогнули проволоку и согнули из неё другой прямоугольник с длиной на 16 % больше, чем раньше. На сколько процентов уменьшилась его ширина?
Ответ: 20%
Задание 2.3 Из куска проволоки согнули прямоугольник, длина которого в 2 раза больше ширины. Затем разогнули проволоку и согнули из неё другой прямоугольник с длиной на 10 % больше, чем раньше. На сколько процентов уменьшилась его ширина?
→ Получить ответы
Задание 3. В каждой клетке квадрата 18×18 лежит монета орлом вверх. Какое наименьшее количество монет нужно перевернуть, чтобы в результате на каждой горизонтали, вертикали и обеих диагоналях были как монеты, лежащие вверх орлом, так и монеты, лежащие вверх решкой?
Ответ: 72
Задание 3.1 В каждой клетке квадрата 12 х 12 лежит монета орлом вверх. Какое наименьшее количество монет нужно перевернуть, чтобы в результате на каждой горизонтали, вертикали и обеих диагоналях были как монеты, лежащие вверх орлом, так и монеты, лежащие вверх решкой?
→ Получить ответы
Задание 3.2 В каждой клетке квадрата 16 х 16 лежит монета орлом вверх. Какое наименьшее количество монет нужно перевернуть, чтобы в результате на каждой горизонтали, вертикали и обеих диагоналях были как монеты, лежащие вверх орлом, так и монеты, лежащие вверх решкой?
Ответ: 162
Задание 3.3 В каждой клетке квадрата 14 х 14 лежит монета орлом вверх. Какое наименьшее количество монет нужно перевернуть, чтобы в результате на каждой горизонтали, вертикали и обеих диагоналях были как монеты, лежащие вверх орлом, так и монеты, лежащие вверх решкой?
→ Получить ответы
Задание 4. В одной из двух канистр содержится 18 литров воды, другая пуста. Из первой канистры во вторую переливают половину имеющейся там воды, затем из второй в первую треть имеющейся там воды, потом из первой во вторую четверть имеющейся там воды и т. д. Сколько воды будет в первой канистре после 997 переливаний? Ответ выразите в литрах.
Ответ: 7 литров
Задание 4.1 В одной из двух канистр содержится 14 литров воды, другая пуста. Из первой канистры вторую переливают половину имеющейся там воды, затем из второй в первую — треть имеющейся там воды, потом из первой во вторую — четверть имеющейся там воды и т. д. Сколько воды будет в первой канистре после 1003 переливаний? Ответ выразите в литрах.
→ Получить ответы
Задание 4.2 В одной из двух канистр содержится 10 литров воды, другая пуста. Из первой канистры во вторую переливают половину имеющейся там воды, затем из второй в первую — треть имеющейся там воды, потом из первой во вторую — четверть имеющейся там воды и т. д. Сколько воды будет в первой канистре после 1001 переливания? Ответ выразите в литрах.
Ответ: 5 литров
Задание 4.3 В одной из двух канистр содержится 20 литров воды, другая пуста. Из первой канистры во вторую переливают половину имеющейся там воды, затем из второй в первую — треть имеющейся там воды, потом из первой во вторую — четверть имеющейся там воды и т. д. Сколько воды будет в первой канистре после 999 переливаний? Ответ выразите в литрах.
→ Получить ответы
Задание 5. Стороны клетчатого многоугольника с периметром 20 , проходят по линиям сетки? Сторона клетки равна 1. Определите минимально возможное количество его вершин.
Определите максимально возможное количество его вершин.
→ Получить ответы
Задание 5.1 Стороны клетчатого многоугольника с периметром 28 , проходят по линиям сетки? Сторона клетки равна 1. Определите минимально возможное количество его вершин.
Определите максимально возможное количество его вершин.
→ Получить ответы
Задание 5.2 Стороны клетчатого многоугольника с периметром 24 , проходят по линиям сетки? Сторона клетки равна 1. Определите минимально возможное количество его вершин.
Определите максимально возможное количество его вершин.
→ Получить ответы
Задание 5.3 Стороны клетчатого многоугольника с периметром 16 , проходят по линиям сетки? Сторона клетки равна 1. Определите минимально возможное количество его вершин.
Определите максимально возможное количество его вершин.
→ Получить ответы
Задание 6. Все числа от 1 до 800 выписали подряд: 123456789101112 … 799800 . Сколько раз в этом ряду сразу после цифры 5 стоит цифра 6?
→ Получить ответы
Задание 6.1 Все числа от 1 до 500 выписали подряд: 123456789101112 … 499500. Сколько раз в этом ряду сразу после цифры 2 стоит цифра 3?
→ Получить ответы
Задание 6.2 Все числа от 1 до 700 выписали подряд: 123456789101112 … 699700. Сколько раз в этом ряду сразу после цифры 4 стоит цифра 5?
→ Получить ответы
Задание 6.3 Все числа от 1 до 600 выписали подряд: 123456789101112 … 599600. Сколько раз в этом ряду сразу после цифры 3 стоит цифра 4?
→ Получить ответы
Задание 7. В клетках таблицы 2×2 записаны положительные числа. Саша и Паша выбрали клетку и заштриховали её серым. Саша посчитал сумму чисел в строке, в которой она находится, а Паша проделал ту же самую операцию для столбца. Потом мальчики перемножили свои суммы и получили результат, в 3 раза больший числа в заштрихованной клетке. Оказалось, что это условие справедливо для любой из четырёх клеток. Найдите сумму всех чисел в таблице.
→ Получить ответы
Задание 7.1 B клетках таблицы 2 х 2 записаны положительные числа. Витя и Женя выбрали клетку и заштриховали её серым. Витя посчитал сумму чисел в строке, в которой она находится, Женя проделал ту же самую операцию для столбца. Потом мальчики перемножили свои суммы и получили результат, в 4 раза меньший числа в заштрихованной клетке. Оказалось, что это условие справедливо для любой из четырёх клеток. Найдите сумму всех чисел в таблице.
→ Получить ответы
Задание 7.2 B клетках таблицы 2 х 2 записаны положительные числа. Петя и Вася выбрали клетку и заштриховали её серым. Петя посчитал сумму чисел в строке, в которой она находится, Вася проделал ту же самую операцию для столбца. Потом мальчики перемножили свои суммы и получили результат, в 2 раза меньший числа в заштрихованной клетке. Оказалось, что это условие справедливо для любой из четырёх клеток. Найдите сумму всех чисел в таблице.
→ Получить ответы
Задание 7.3 B клетках таблицы 2 х 2 записаны положительные числа. Толя и Рома выбрали клетку и заштриховали её серым. Толя посчитал сумму чисел в строке, в которой она находится, Рома проделал ту же самую операцию для столбца. Потом мальчики перемножили свои суммы и получили результат, в 5 раз больший числа в заштрихованной клетке. Оказалось, что это условие справедливо для любой из четырёх клеток. Найдите сумму всех чисел в таблице.
→ Получить ответы
Задание 8. По контуру квадрата в одном направлении ползут три жука, скорости которых постоянны и различны. Найдите скорость самого медленного из жуков, если скорости других равны 20 мм/с и 60 мм/с, а все обгоны происходят только в вершинах квадрата. Ответ выразите в мм/с.
→ Получить ответы
Задание 8.1 По контуру квадрата в одном направлении ползут три жука, скорости которых постоянны и различны. Найдите скорость самого медленного из жуков, если скорости других равны 10 мм/с и 30 мм/с, а все обгоны происходят только в вершинах квадрата. Ответ выразите в мм/с.
→ Получить ответы
Задание 8.2 По контуру квадрата в одном направлении ползут три жука, скорости которых постоянны и различны. Найдите скорость самого медленного из жуков, если скорости других равны 15 мм/с и 45 мм/с, а все обгоны происходят только в вершинах квадрата. Ответ выразите в мм/с.
→ Получить ответы
Задание 8.3 По контуру квадрата в одном направлении ползут три жука, скорости которых постоянны и различны. Найдите скорость самого медленного из жуков, если скорости других равны 25 мм/с и 75 мм/с, а все обгоны происходят только в вершинах квадрата. Ответ выразите B мм/с.
8 класс
Задание 1. Три одноклассника вернулись в школу с игры в футбол. Учитель спросил у каждого, сколько они вместе забили мячей, и дети ответили следующее. Семён: «Больше пяти»; Дима: «Больше девяти»; Миша: «Больше шести». Сколько могло быть забито мячей, если известно, что два одноклассника сказали правду, а третий солгал? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
1.2. Три одноклассника вернулись в школу с игры в футбол. Учитель спросил у каждого, сколько они вместе забили мячей, и дети ответили следующее. Семён: «Больше пяти»; Дима: «Больше девяти»; Миша: «Больше шести». Сколько могло быть забито мячей, если известно, что два одноклассника сказали правду, а третий солгал? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
→ Получить ответы
Задание 2. Пусть A двузначное число, не кратное 10, B трёхзначное число. Известно, что A процентов от B равны 400. Найдите A и B .
2.2. Пусть A — двузначное число, не кратное 10, B — четырёхзначное число. Известно, что A процентов от B равны 200. Найдите A и B.
2.3. Пусть A — двузначное число, не кратное 10, B — трёхзначное число. Известно, что A процентов от B равны 320. Найдите A и B.
→ Получить ответы
Задание 3. Вася нарисовал в тетради четырёхугольник, а затем измерил линейкой четыре его стороны и одну из диагоналей. Получившиеся пять чисел Вася записал по возрастанию: 1, 2, 2.8, 5, 7.5.
3.2. Даша нарисовала в тетради четырёхугольник, а затем измерила линейкой четыре его стороны и одну из диагоналей. Получившиеся пять чисел Даша записала по возрастанию: 2, 3, 4.3, 8, 12.1.
Какое из этих чисел может являться длиной диагонали?
→ Получить ответы
1.2. Три одноклассника вернулись в школу с игры в футбол. Учитель спросил у каждого, сколько они вместе забили мячей, и дети ответили следующее. Семён: «Больше пяти»; Дима: «Больше девяти»; Миша: «Больше шести». Сколько могло быть забито мячей, если известно, что два одноклассника сказали правду, а третий солгал? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
→ Получить ответы
Задание 2. Пусть A двузначное число, не кратное 10, B трёхзначное число. Известно, что A процентов от B равны 400. Найдите A и B .
2.2. Пусть A — двузначное число, не кратное 10, B — четырёхзначное число. Известно, что A процентов от B равны 200. Найдите A и B.
2.3. Пусть A — двузначное число, не кратное 10, B — трёхзначное число. Известно, что A процентов от B равны 320. Найдите A и B.
→ Получить ответы
Задание 3. Вася нарисовал в тетради четырёхугольник, а затем измерил линейкой четыре его стороны и одну из диагоналей. Получившиеся пять чисел Вася записал по возрастанию: 1, 2, 2.8, 5, 7.5.
3.2. Даша нарисовала в тетради четырёхугольник, а затем измерила линейкой четыре его стороны и одну из диагоналей. Получившиеся пять чисел Даша записала по возрастанию: 2, 3, 4.3, 8, 12.1.
Какое из этих чисел может являться длиной диагонали?
→ Получить ответы
Задание 4. В треугольнике ABC угол между биссектрисой и высотой, проведёнными из вершины B, равен 15∘, а угол C равен 25∘ . Найдите угол A. Ответ выразите в градусах. Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
4.1. В треугольнике ABC угол между биссектрисой и высотой, проведёнными из вершины B, равен 30°, а угол C равен 20°. Найдите угол A. Ответ выразите в градусах. Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
4.2. В треугольнике ABC угол между биссектрисой и высотой, проведёнными из вершины B, равен 25°, а угол C равен 15°. Найдите угол A. Ответ выразите в градусах. Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
→ Получить ответы
Задание 5. Даниил придумал натуральное число. После этого он вычел из него сумму его цифр. Потом из полученного числа он снова вычел сумму его цифр и так далее. После четырнадцати таких вычитаний впервые получился ноль. Какое наименьшее число мог придумать Даниил?
Какое наибольшее число мог придумать Даниил?
5.2. Сергей придумал натуральное число. После этого он вычел из него сумму его цифр. Потом из полученного числа он снова вычел сумму его цифр и так далее. После двенадцати таких вычитаний впервые получился ноль. Какое наименьшее число мог придумать Сергей? Какое наибольшее число мог придумать Сергей?
→ Получить ответы
Задание 6. Некоторое четырёхзначное число является квадратом числа x. Если же цифры этого четырёхзначного числа записать в обратном порядке, то получится квадрат числа y, причём y кратно x и y>x. Найдите y2 .
6.2. Некоторое четырёхзначное число является квадратом числа x. Если же цифры этого четырёхзначного числа записать в обратном порядке, то получится квадрат числа y, причём y кратно x и y > x. Найдите x².
→ Получить ответы
Задание 7. На доске записано семизначное число, состоящее из различных цифр, не равных нулю. Разрешается добавить в это число любую цифру, записав её в любом месте между цифрами данного числа, а также в начале или в конце числа. Сколько различных восьмизначных чисел может получиться?
→ Получить ответы
Задание 8. Найдите все натуральные n<70, для которых числа n+18n и nn+18 записываются в виде конечных десятичных дробей. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
8.2. Найдите все натуральные n < 70, для которых числа (n + 21)/n = n/(n + 21) записываются в виде конечных десятичных дробей. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
4.1. В треугольнике ABC угол между биссектрисой и высотой, проведёнными из вершины B, равен 30°, а угол C равен 20°. Найдите угол A. Ответ выразите в градусах. Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
4.2. В треугольнике ABC угол между биссектрисой и высотой, проведёнными из вершины B, равен 25°, а угол C равен 15°. Найдите угол A. Ответ выразите в градусах. Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
→ Получить ответы
Задание 5. Даниил придумал натуральное число. После этого он вычел из него сумму его цифр. Потом из полученного числа он снова вычел сумму его цифр и так далее. После четырнадцати таких вычитаний впервые получился ноль. Какое наименьшее число мог придумать Даниил?
Какое наибольшее число мог придумать Даниил?
5.2. Сергей придумал натуральное число. После этого он вычел из него сумму его цифр. Потом из полученного числа он снова вычел сумму его цифр и так далее. После двенадцати таких вычитаний впервые получился ноль. Какое наименьшее число мог придумать Сергей? Какое наибольшее число мог придумать Сергей?
→ Получить ответы
Задание 6. Некоторое четырёхзначное число является квадратом числа x. Если же цифры этого четырёхзначного числа записать в обратном порядке, то получится квадрат числа y, причём y кратно x и y>x. Найдите y2 .
6.2. Некоторое четырёхзначное число является квадратом числа x. Если же цифры этого четырёхзначного числа записать в обратном порядке, то получится квадрат числа y, причём y кратно x и y > x. Найдите x².
→ Получить ответы
Задание 7. На доске записано семизначное число, состоящее из различных цифр, не равных нулю. Разрешается добавить в это число любую цифру, записав её в любом месте между цифрами данного числа, а также в начале или в конце числа. Сколько различных восьмизначных чисел может получиться?
→ Получить ответы
Задание 8. Найдите все натуральные n<70, для которых числа n+18n и nn+18 записываются в виде конечных десятичных дробей. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
8.2. Найдите все натуральные n < 70, для которых числа (n + 21)/n = n/(n + 21) записываются в виде конечных десятичных дробей. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
9 класс
Задание 1. Жора решал уравнение 19x=b, где неизвестная переменная x, а b некоторое число. Когда он увеличил коэффициент при x и число в правой части на 1, корень уравнения тоже увеличился на 1. На сколько увеличился бы корень уравнения, если бы Жора вместо этого увеличил коэффициент при x и число в правой части на 3?
Ответ: 4,67
Задание 1.1 Жора решал уравнение 11x = b, где неизвестная переменная 2, а b — некоторое число. Когда он увеличил коэффициент при х и число в правой части на 1, корень уравнения тоже увеличился на 1. На сколько увеличился бы корень уравнения, если бы Жора вместо этого увеличил коэффициент при 2 и число в правой части на 7?
Задание 1.2 Жора решал уравнение 13х = 6, где неизвестная переменная х, а в — некоторое число. Когда он увеличил коэффициент при х и число в правой части на 1, корень уравнения тоже увеличился на 1. На сколько увеличился бы корень уравнения, если бы Жора вместо этого увеличил коэффициент при х и число в правой части на 5?
Ответ: 35/9
Задание 2. Про натуральное число A известно, что оно делится на 50 и не делится на 75, а про натуральное число B известно, что оно делится на 60 и не делится на 90. Какие утверждения о числе C=A−B могут быть верны? Выберите все подходящие варианты:
C делится на 100
C не делится на 75
C не делится на 10
C делится на 6
C делится на 5
Задание 2.1 Про натуральное число А известно, что оно делится на 24 и не делится на 36, а про натуральное число В известно, что оно делится на 30 и не делится на 60. Какие утверждения о числе C = A — B могут быть верны? Выберите все подходящие варианты:
- С делится на 6
- C не делится на 12
- С делится на 4
- С не делится на 35
- C не делится на 3
Ответ: 1, 2, 4 — верны
Задание 2.2 Про натуральное число А известно, что оно делится на 60 и не делится на 90, а про натуральное число В известно, что оно делится на 36 и не делится на 48. Какие утверждения о числе C = А — В могут быть верны? Выберите все подходящие варианты:
- С делится на 18
- С не делится на 4
- С не делится на 9
- С делится на 6
- С не делится на 20
Задание 3. У Ивана есть большая корзина с 940 шариками одинакового размера. Как минимум один из шариков красный, остальные — зелёные. Иван вычислил, что вероятность того, что два случайно выбранных шарика окажутся красными, совпадает с вероятностью того, что они будут разного цвета. Сколько красных шариков в корзине?
Ответ: 627
Задание 3.1 У Ивана есть большая корзина с 970 шариками одинакового размера. Как минимум один из шариков красный, остальные зелёные. Иван вычислил, что вероятность того, что два случайно выбранных шарика окажутся красными, совпадает с вероятностью того, что они будут разного цвета. Сколько красных шариков в корзине?
Задание 3.2 У Ивана есть большая корзина с 880 шариками одинакового размера. Как минимум один из шариков красный, остальные зелёные. Иван вычислил, что вероятность того, что два случайно выбранных шарика окажутся красными, совпадает с вероятностью того, что они будут разного цвета. Сколько красных шариков в корзине?
Ответ: 587
Задание 4. Периметр трапеции ABCD (AD BC) равен 60, а расстояние между основаниями — 7 длина отрезка AB указана на рисунке.
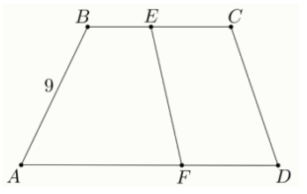
Периметры четырёхугольников ABEF и CDFE равны; площади этих четырёхугольников также равны.
Найдите длину отрезка CD.
Найдите площадь четырёхугольника ABCD.
Задание 4.1 Периметр трапеции ABCD (AD BC) равен 90, а расстояние между основаниями — 6 длина отрезка AB указана на рисунке.
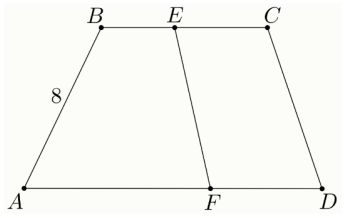
Периметры четырёхугольников ABEF и CDFE равны; площади этих четырёхугольников также равны.
Найдите длину отрезка CD.
Найдите площадь четырёхугольника ABCD.
Задание 4.2 Периметр трапеции ABCD (AD BC) равен 80, а расстояние между основаниями — 4 длина отрезка AB указана на рисунке.
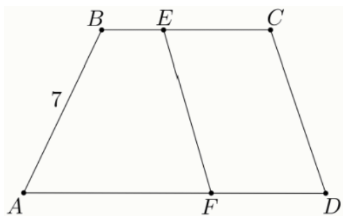
Периметры четырёхугольников ABEF и CDFE равны; площади этих четырёхугольников также равны.
Найдите длину отрезка CD.
Найдите площадь четырёхугольника ABCD.
Задание 5. Про действительные числа a, b и c известно, что 2⋅(2a√5+b√15+c√19)=a2+b2+c2+54.
Найдите значение выражения a2+b2+2c2.
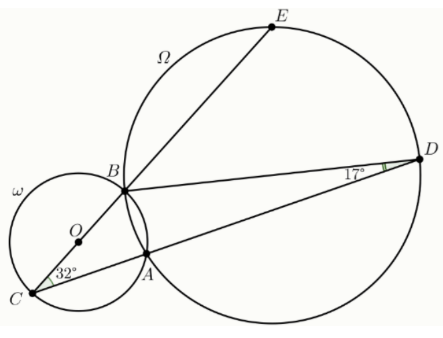
Задание 6. Окружности Ω и ω пересекаются в точках A и B O центр окружности ω. Лучи CA и CB пересекают окружность Ω в точках D и E соответственно. Оказалось, что точка OК лежит на отрезке EC. На рисунке указаны значения углов ∠BCA и ∠BDA. Найдите градусную меру угла ∠EAB.
Задание 7. На большой клетчатой плоскости можно размещать прямоугольники размером 4×9 так, что каждый прямоугольник покрывает ровно 36 клеток. Прямоугольники можно размещать как горизонтально, так и вертикально, при этом они могут перекрываться
Найдите наибольшее целое число N, при котором невозможно покрыть ровно N клеток таким способом.
Задание 8. Исследователи опросили N человек, чтобы узнать, какие из трёх продуктов по уходу за кожей A , B , C они используют. Результаты опроса: 39 человек используют B; 59 человек НЕ пользуются A ; 24 человека НЕ пользуются C; 58 человек используют как минимум два из трёх видов A, B , C. Каждый человек мог выбрать любую комбинацию средств (в том числе не выбрать ни одно). Найдите минимально возможное значение N.
10 класс
Задание 1. У Жоры есть два правильных многоугольника, причём у большего на 8 сторон больше, чем у меньшего. Внутренние углы этих многоугольников отличаются на 1.5∘. Сколько сторон у меньшего многоугольника?
Ответ: 45
Задание 1.1 У Жоры есть два правильных многоугольника, причём у большего на 8 сторон больше, чем у меньшего. Внутренние углы этих многоугольников отличаются на 0.5°. Сколько сторон у меньшего многоугольника?
Задание 2. В некотором городе погода бывает только двух видов: солнечная или дождливая. Если сегодня солнечно, то завтра с вероятностью 34 снова будет солнечно. Если сегодня дождливо, то завтра с вероятностью 1\3 будет солнечно. Сегодня пятница и на улице солнечно. На воскресенье запланирована поездка на природу. Какова вероятность того, что в воскресенье будет солнечно?
Ответ: 11/16
Задание 2.1 В некотором городе погода бывает только двух видов: солнечная или дождливая. Если сегодня солнечно, то завтра с вероятностью 4 снова будет солнечно. Если сегодня дождливо, то завтра с вероятностью 2 будет солнечно. Сегодня пятница и на улице солнечно. На воскресенье запланирована поездка на природу. Какова вероятность того, что в воскресенье будет солнечно?
Задание 3. На склад поступили 11 11 шаров разного диаметра: 25 , 20, 26, 24, 17, 26, 26, 12, 16, 26, 12. А также 11 кубических коробок, у каждой задана длина ребра: 26, 20, 21 , 10, 12 , 18, 17 , 23 , 12 , 19 , 21. Упаковщик может положить шар только в такую коробку, длина ребра которой не меньше диаметра шара. Каждый шар можно упаковать только в одну коробку, и в каждую коробку можно положить не более одного шара. Какое наибольшее количество шаров удастся упаковать?
Задание 3.1 На склад поступили 11 шаров разного диаметра: 12, 23, 12, 18, 27, 10, 12, 16, 27, 19, 16. А также 11 кубических коробок, у каждой задана длина ребра: 11, 26, 28, 15, 11, 13, 17, 14, 19, 28, 13. Упаковщик может положить шар только в такую коробку, длина ребра которой не меньше диаметра шара. Каждый шар можно упаковать только в одну коробку, и в каждую коробку можно положить не более одного шара. Какое наибольшее количество шаров удастся упаковать?
Задание 3.2 На склад поступили 11 шаров разного диаметра: 23, 21, 11, 16, 24, 20, 11, 14, 25, 14, 20. А также 11 кубических коробок, у каждой задана длина ребра: 25, 10, 13, 14, 26, 20, 25, 12, 23, 13, 12. Упаковщик может положить шар только в такую коробку, длина ребра которой не меньше диаметра шара. Каждый шар можно упаковать только в одну коробку, и в каждую коробку можно положить не более одного шара. Какое наибольшее количество шаров удастся упаковать?
Задание 4. На бирже 13 компаний. Для каждой пары компаний верно, что ровно одна из них купила акции другой: либо компания A вложилась в компанию B, либо компания B вложилась в компанию A. Одна из компаний известна под названием «Альфа». Выберите все утверждения, которые обязательно верны: Есть компания, которая вложилась ровно в 6 других компаний Существует компания, которая вложилась как минимум в 6 других В компанию «Альфа» инвестировали не более 5 других Как минимум 12 компаний получили инвестиции хотя бы от одной другой
Задание 5. Какое наименьшее значение принимает функция f(f(f(x))), если f(x)=x2+16x+61?
Задание 5.1 Какое наименьшее значение принимает функция f(f(f(x))), если f(x) = x2+12x+34?
Задание 5.2 Какое наименьшее значение принимает функция f(f(f(x))), если f(x) = x2+12x+47?
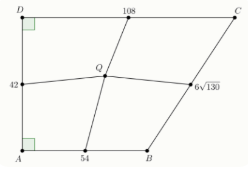
Задание 6. На чертеже представлена трапеция, у которой указаны длины сторон, а также указано, что некоторые углы прямые. Точка Q соединена с серединами всех четырёх сторон трапеции. Четыре образовавшихся четырёхугольника равновелики (то есть имеют одинаковую площадь).
Найдите расстояние от точки Q до стороны AB.
Найдите длину отрезка AQ.
Задание 7. У Жоры есть положительная несократимая дробь, числителем которой является натуральное число.
- Если Жора увеличит и числитель, и знаменатель дроби на некоторое число n, то значение дроби увеличится в 4 раза, а если уменьшит на n, то увеличится в 5 раз. Найдите n.
- Если Жора увеличит и числитель, и знаменатель дроби на некоторое число n, то значение дроби увеличится в 6 раз, а если уменьшит на n, то увеличится в 7 раз. Найдите n.
- Если Жора увеличит и числитель, и знаменатель дроби на некоторое число n, то значение дроби увеличится в 3 раза, а если уменьшит на n, то увеличится в 4 раза. Найдите n.
Задание 8. У Саши и Юры есть по игральному кубику. Одна грань кубика Саши пустая, а на других написаны числа 10,3,8, 14, 1. Одна грань кубика Юры тоже пустая, а на других написаны числа 16, 17 ,13 , 6, 21. Юра выбирает натуральное число N, записывает его на пустые грани обоих кубиков, а потом мальчики бросают свои кубики. Выигрывает тот, у кого выпадет большее число; при равенстве очков объявляется ничья. Какое значение N может выбрать Юра, чтобы вероятность его победы была наибольшей? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
Задание 8. У Саши и Юры есть по игральному кубику. Одна грань кубика Саши пустая, а на других написаны числа 10, 3, 12, 15, 1. Одна грань кубика Юры тоже пустая, а на других написаны числа 18, 19, 14, 6, 21. Юра выбирает натуральное число №, записывает его на пустые грани обоих кубиков, а потом мальчики бросают свои кубики. Выигрывает тот, у кого выпадет большее число; при равенстве очков объявляется ничья. Какое значение № может выбрать Юра, чтобы вероятность его победы была наибольшей? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
11 класс
Задание 1. На доске была написана невозрастающая последовательность натуральных чисел a1⩾a2⩾…⩾a5. Саша написал на листочке другую последовательность: сколько среди ai чисел, больших или равных 1, сколько больше или равных 2и далее до тех пор, пока ему не пришлось бы написать 0 0 . Юра стёр числа с доски. На листочке у Саши остались числа 5, 4, 2 , 2 , 1 , 1 . Какая последовательность была записана на доске?
Задание 2. У Жоры есть три одинаковые колоды, в каждой 6 карточек с числами от 1 до 6. Сначала он наугад вытаскивает по одной карточке из первых двух колод. Если числа на них совпадают, он дополнительно вытаскивает наугад карточку из третьей колоды. Какова вероятность того, что сумма всех вытащенных чисел окажется чётной?
Задание 3. Юра выложил в ряд 2025 монет. Если он уберёт первые две трети монет слева, то как минимум половина из оставшихся окажется лежащей орлом вверх. То же самое происходит, если Юра убирает последние 20 % монет справа среди оставшихся как минимум половина повёрнута орлом вверх. Какое минимальное количество монет может лежать орлом вверх?
Задание 4. На сторонах AC и BC , а также на продолжении стороны AB равностороннего треугольника ABC отмечены точки F , D и E соответственно так, что D середина EF . Длины отрезков BD и DC приведены на рисунке.
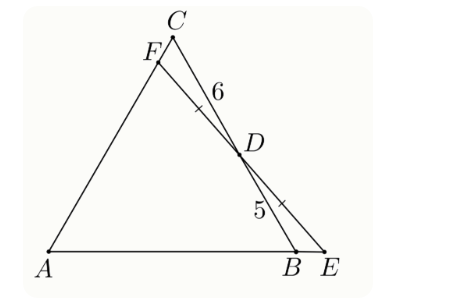
Найдите EF2.
Задание 5. Коэффициенты многочлена P(x) неотрицательные целые числа. Известно, что
P(2)=100P(2)=100,
P(P(2))=102041522.
Найдите значение P(0).
Найдите значение P(1).
Задание 6. Наташа и Петя играют в игру. Вначале Наташа первой называет целое число от 1 до 69 . Затем Петя называет своё число от 1 до 51 . После этого Наташа называет число от 1 до 54 . Если сумма всех трёх названных чисел делится на 68, побеждает Наташа. Иначе побеждает Петя. Какое число Наташа должна назвать первым, чтобы при любом выборе Пети она могла победить? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
Задание 7. Пусть x, y, z такие положительные действительные числа, что выполнены следующие равенства:
- xlog2(yz)=212⋅58,
- ylog2(zx)=26⋅52,
- zlog2(xy)=210⋅510.
Найдите значение произведения xyz Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
Задание 8. Одинаковые ветряные турбины расположены на одинаковом расстоянии d друг от друга вдоль прямой линии. Каждая башня турбины представляет собой вертикальный цилиндр радиусом 1.5 метра. Пусть прямая, проходящая через центры оснований всех башен. Наблюдатель находится в точке O на той же плоскости, причём проекция O на l совпадает с одним из центров турбины, расстояние от точки O до точки l на рисунке.
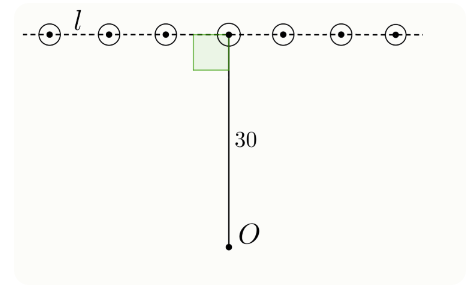
При разных значениях d число полностью видимых башен может быть разным. Найдите наибольшее число башен, которые могут быть полностью видны.
Башня T полностью видна, если отрезки касательных из точки O до башни T не пересекают (но могут касаться) другие башни. Башен очень много в обе стороны от наблюдателя.
Часть ответов по ВсОШ публикуется бесплатно в нашем Telegram-канале: @shcolaotvet