14.10.2025 — ВСОШ СИРИУС Школьный этап по Математике 7-11 класс: задания и ответы для 2 группы и 77 региона
Авторские решения к этой работе доступны для покупки на нашем сайте:
Группа №2 включает регионы: Белгородская область (31), Брянская область (32), Владимирская область (33), Воронежская область (36), город Санкт-Петербург (78), Ивановская область (37), Калининградская область (39), Калужская область (40), Кировская область (43), Костромская область (44), Курская область (46), Ленинградская область (47), Липецкая область (48), Нижегородская область (52), Орловская область (57), Республика Марий Эл (12), Республика Мордовия (13), Республика Татарстан (16), Республика Чувашия (21), Рязанская область (62), Смоленская область (67), Тамбовская область (68), Тверская область (69), Тульская область (71), Ярославская область (76).
Рассмотрим задания и ответы по Математике для 7–11 классов:
Навигация
7 класс
Задание 1. На спортивных соревнованиях по энерджиболу матч длится 44 минуты, а на поле одновременно присутствуют 5 игроков. В составе команды «Альфа» 8 игроков. Тренер команды хочет, чтобы все игроки провели на поле одинаковое количество времени. Сколько времени каждый игрок должен провести на поле, если количество замен не ограничено?
Задание 1.1 На спортивных соревнованиях по энерджиболу матч длится 52 минуты, а на поле одновременно присутствуют 5 игроков. В составе команды «Альфа» 8 игроков. Тренер команды хочет, чтобы все игроки провели на поле одинаковое количество времени. Сколько времени каждый игрок должен провести на поле, если количество замен не ограничено?
Задание 1.2 На спортивных соревнованиях по энерджиболу матч длится 60 минуты, а на поле одновременно присутствуют 5 игроков. В составе команды «Альфа» 8 игроков. Тренер команды хочет, чтобы все игроки провели на поле одинаковое количество времени. Сколько времени каждый игрок должен провести на поле, если количество замен не ограничено?
Задание 1.3 На спортивных соревнованиях по энерджиболу матч длится 68 минуты, а на поле одновременно присутствуют 5 игроков. В составе команды «Альфа» 8 игроков. Тренер команды хочет, чтобы все игроки провели на поле одинаковое количество времени. Сколько времени каждый игрок должен провести на поле, если количество замен не ограничено?
- 27 минут
- 27 минут 30 секунд
- 32 минуты
- 32 минуты 30 секунд
- 37 минут
- 37 минут 30 секунд
- 42 минуты
- 42 минуты 30 секунд
Задание 2. Площадь квадрата, изображённого на рисунке, равна 240 см2. Точка O — центр квадрата, а точка M — середина его стороны.
Задание 2.1 Площадь квадрата, изображённого на рисунке, равна 320 см2. Точка O — центр квадрата, а точка M — середина его стороны.
Задание 2.2 Площадь квадрата, изображённого на рисунке, равна 280 см2. Точка O — центр квадрата, а точка M — середина его стороны.
Задание 2.3 Площадь квадрата, изображённого на рисунке, равна 200 см2. Точка O — центр квадрата, а точка M — середина его стороны.
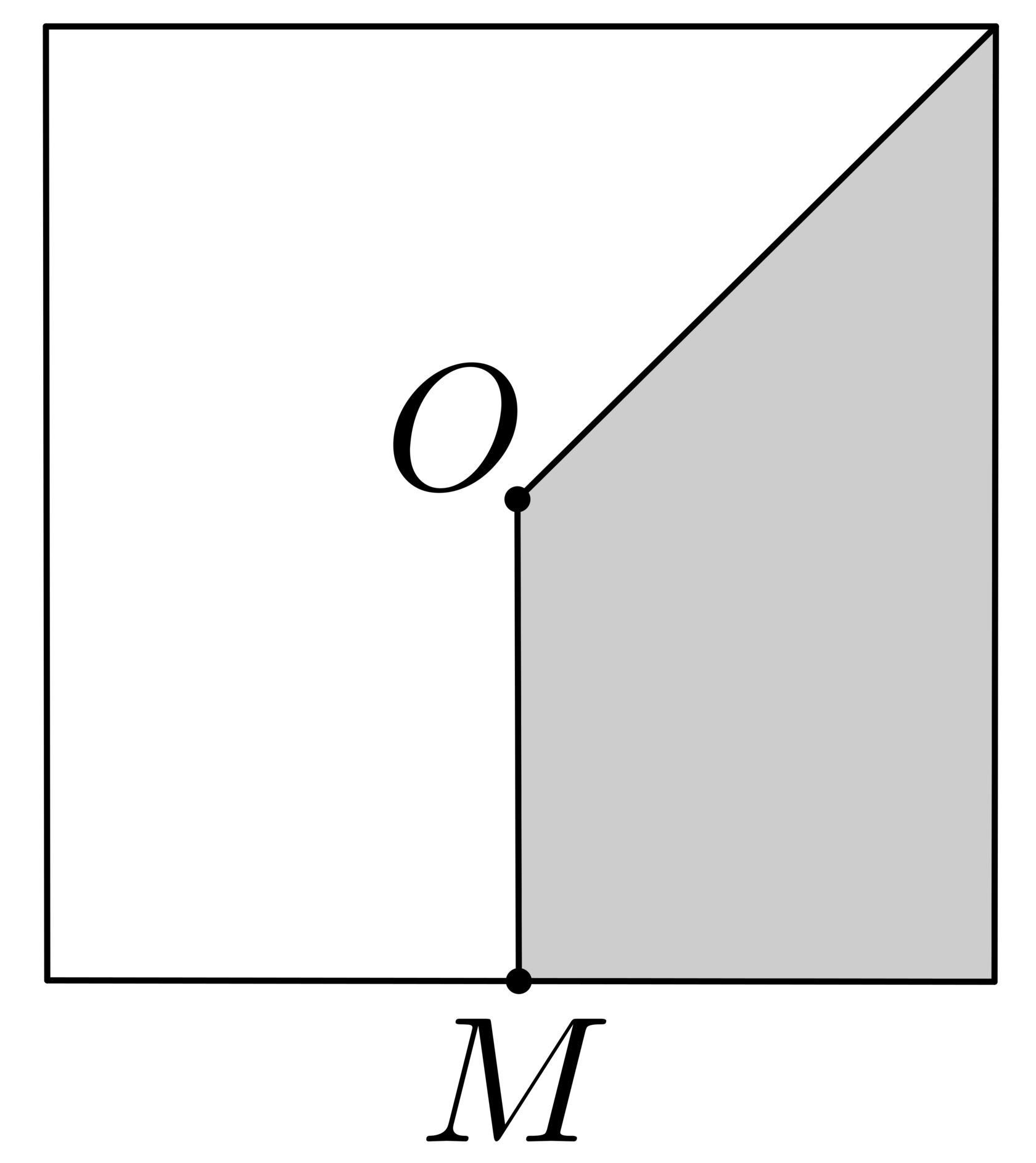
Чему равна площадь серой части?
Задание 3. На карте точками обозначены города, а линиями дороги.
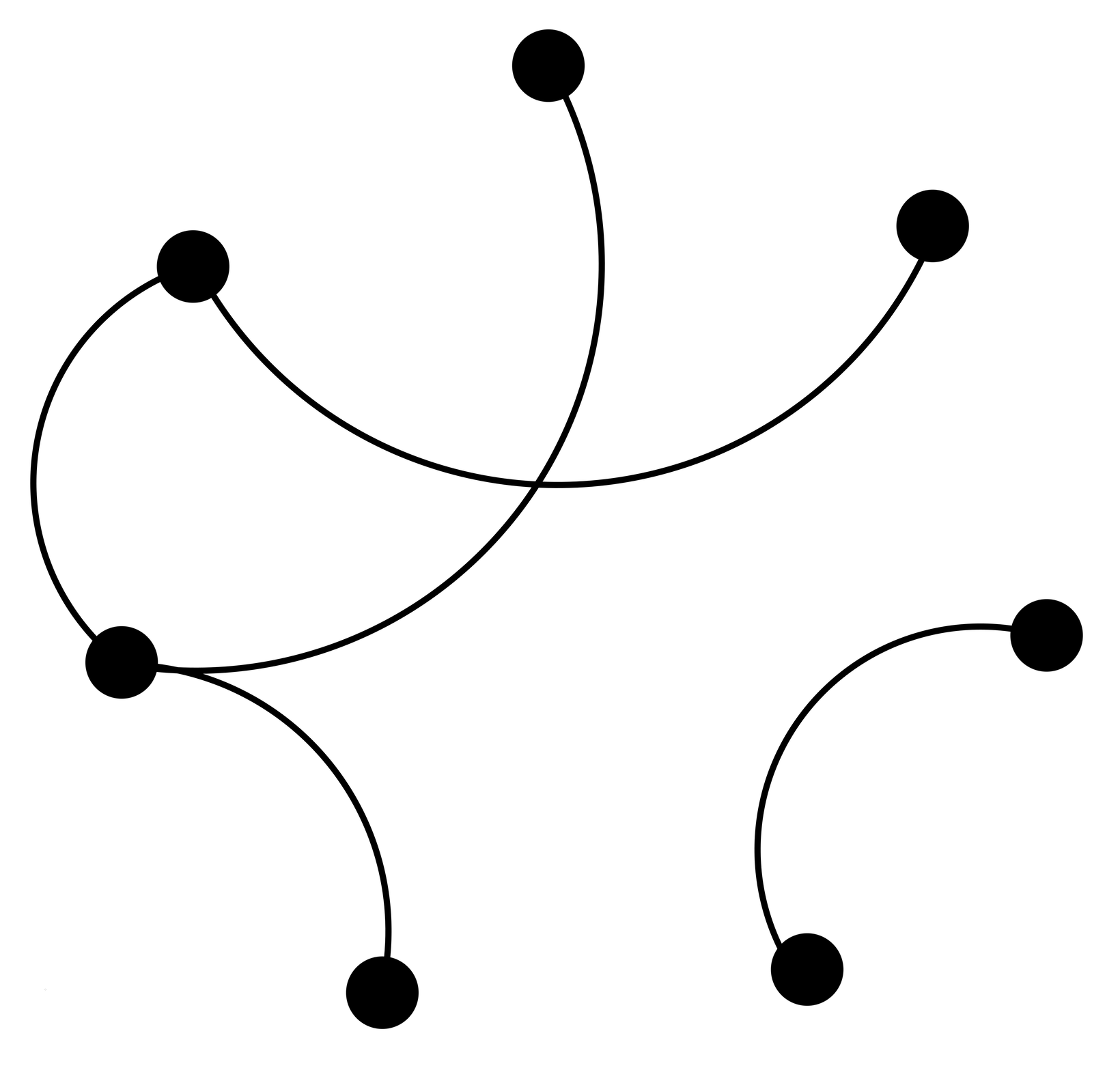
Какое наименьшее число дорог нужно добавить, чтобы из городов выходило поровну дорог?
Задание 3.1 На карте точками обозначены города, а линиями дороги.
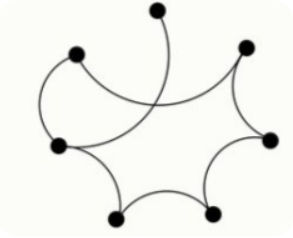
Какое наименьшее число дорог нужно добавить, чтобы из городов выходило поровну дорог?
Задание 3.2 На карте точками обозначены города, а линиями дороги.
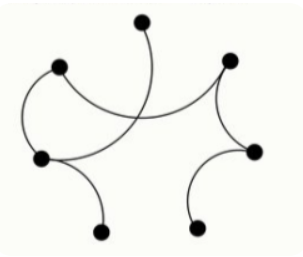
Какое наименьшее число дорог нужно добавить, чтобы из городов выходило поровну дорог?
Задание 3.3 На карте точками обозначены города, а линиями дороги.
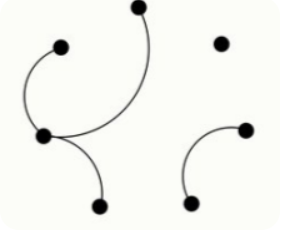
Какое наименьшее число дорог нужно добавить, чтобы из городов выходило поровну дорог?
Задание 4. На острове рыцарей и лжецов, где рыцари всегда говорят правду, а лжецы — лгут, встретились четыре жителя — Антон, Иван, Пётр и Богдан.
Богдан сказал: «Антон — лжец!».
Антон сказал: «Иван — рыцарь!».
Иван сказал: «Я знаю точно, что в паре Богдана и Петра один человек рыцарь, а другой лжец».
Пётр сказал: «Богдан — лжец!».
Задание 4.1 На острове рыцарей и лжецов, где рыцари всегда говорят правду, а лжецы — лгут, встретились четыре жителя — Антон, Иван, Пётр и Богдан.
Петр сказал: «Антон — лжец!».
Антон сказал: «Богдан — рыцарь!».
Богдан сказал: «Я знаю точно, что в паре Петр и Иван один человек рыцарь, а другой лжец».
Иван сказал: «Петр— лжец!».
Задание 4.2 На острове рыцарей и лжецов, где рыцари всегда говорят правду, а лжецы — лгут, встретились четыре жителя — Антон, Иван, Пётр и Богдан.
Иван сказал: «Богдан— лжец!».
Богдан сказал: «Петр— рыцарь!».
Петр сказал: «Я знаю точно, что в паре Ивана и Антона один человек рыцарь, а другой лжец».
Пётр сказал: «Иван — лжец!».
Задание 4.3 На острове рыцарей и лжецов, где рыцари всегда говорят правду, а лжецы — лгут, встретились четыре жителя — Антон, Иван, Пётр и Богдан.
Антон сказал: «Иван — лжец!».
Иван сказал: «Петр — рыцарь!».
Петр сказал: «Я знаю точно, что в паре Богдана и Антона один человек рыцарь, а другой лжец».
Богдан сказал: «Антон — лжец!».
Кем является каждый из собеседников?
- Антон
- Иван
- Богдан
- Пётр
- Рыцарь
- Лжец
Задание 5. Саша составляет список из 100 чисел по следующему правилу: первое число в списке равно 2028 второе число равно 1, каждое следующее получается так: из последнего записанного числа вычитается предпоследнее и прибавляется 5. Например, третье число равно −2022, потому что 1−2028+5=−2022. Найдите сумму 100 первых чисел из списка Саши.
Задание 5.1 Саша составляет список из 100 чисел по следующему правилу: первое число в списке равно 2026 второе число равно 1, каждое следующее получается так: из последнего записанного числа вычитается предпоследнее и прибавляется 5. Например, третье число равно −2020, потому что 1−2026+5=−2020. Найдите сумму 100 первых чисел из списка Саши.
Задание 5.2 Саша составляет список из 100 чисел по следующему правилу: первое число в списке равно 2025 второе число равно 1, каждое следующее получается так: из последнего записанного числа вычитается предпоследнее и прибавляется 5. Например, третье число равно −2019, потому что 1−2025+5=−2019. Найдите сумму 100 первых чисел из списка Саши.
Задание 5.3 Саша составляет список из 100 чисел по следующему правилу: первое число в списке равно 2027 второе число равно 1, каждое следующее получается так: из последнего записанного числа вычитается предпоследнее и прибавляется 5. Например, третье число равно −2021, потому что 1−2027+5=−2021. Найдите сумму 100 первых чисел из списка Саши.
Задание 6. В тетрадь записаны последовательные целые числа от 1 до 107 ручками двух цветов: красной и синей. Оказалось, что наибольшее число, записанное синим цветом, равно количеству чисел, записанных синим цветом. А наименьшее число, записанное красным цветом, равно половине от количества чисел, записанных красным цветом. Сколько чисел записано красным цветом?
Задание 6.1 В тетрадь записаны последовательные целые числа от 1 до 110 ручками двух цветов: красной и синей. Оказалось, что наибольшее число, записанное синим цветом, равно количеству чисел, записанных синим цветом. А наименьшее число, записанное красным цветом, равно половине от количества чисел, записанных красным цветом. Сколько чисел записано красным цветом?
Задание 6.2 В тетрадь записаны последовательные целые числа от 1 до 101 ручками двух цветов: красной и синей. Оказалось, что наибольшее число, записанное синим цветом, равно количеству чисел, записанных синим цветом. А наименьшее число, записанное красным цветом, равно половине от количества чисел, записанных красным цветом. Сколько чисел записано красным цветом?
Задание 6.3 В тетрадь записаны последовательные целые числа от 1 до 104 ручками двух цветов: красной и синей. Оказалось, что наибольшее число, записанное синим цветом, равно количеству чисел, записанных синим цветом. А наименьшее число, записанное красным цветом, равно половине от количества чисел, записанных красным цветом. Сколько чисел записано красным цветом?
8 класс
Задание 1. Однажды в солнечный день Аля пошла гулять на стадион, а Валя — в парк. Аля двигалась в полтора раза быстрее подруги и прошла в два раза большее расстояние, чем Валя. Прогулка Али заняла на 40 минут больше, чем прогулка Вали. Сколько времени гуляла Аля? Ответ выразите в минутах.
Задание 1.1 Однажды в солнечный день Аля пошла гулять на стадион, а Валя — в парк. Аля двигалась в два раза быстрее подруги и прошла в пять раз большее расстояние, чем Валя. Прогулка Али заняла на 45 минут больше, чем прогулка Вали. Сколько времени гуляла Аля? Ответ выразите в минутах.
Задание 1.2 Однажды в солнечный день Аля пошла гулять на стадион, а Валя — в парк. Аля двигалась в два раза быстрее подруги и прошла в полтора раза большее расстояние, чем Валя. Прогулка Али заняла на 35 минут меньше, чем прогулка Вали. Сколько времени гуляла Аля? Ответ выразите в минутах.
Задание 1.3 Однажды в солнечный день Аля пошла гулять на стадион, а Валя — в парк. Аля двигалась в полтора раза быстрее подруги и прошла в четыре раза большее расстояние, чем Валя. Прогулка Али заняла на 3 часа 20 минут больше, чем прогулка Вали. Сколько времени гуляла Аля? Ответ выразите в минутах.
Задание 2. На рисунке выберите несколько из отмеченных точек так, чтобы на каждой из шести прямых было выбрано ненулевое чётное количество точек.
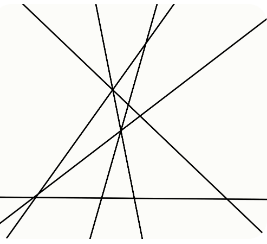
Задание 3. В треугольнике ABC угол B равен 146∘, а высота, опущенная из вершины A, в два раза меньше биссектрисы угла A. Найдите угол C. Ответ выразите в градусах.
Задание 3.1 В треугольнике АВС угол В равен 152°, а высота, опущенная из вершины А, в два раза меньше биссектрисы угла А. Найдите угол С. Ответ выразите в градусах.
Задание 3.2 В треугольнике АВС угол В равен 142°, а высота, опущенная из вершины А, в два раза меньше биссектрисы угла А. Найдите угол С. Ответ выразите в градусах.
Задание 3.3 В треугольнике АВС угол В равен 134°, а высота, опущенная из вершины А, в два раза меньше биссектрисы угла А. Найдите угол С. Ответ выразите в градусах.
Задание 4. Таблицу 5×5 разбили на 7 частей по линиям сетки так, чтобы клетки внутри одного фрагмента граничили только по горизонтали или по вертикали.
В каждой части в одной из клеток написали количество клеток в этом фрагменте. Отметьте на изображении все клетки фрагмента, содержащего выделенную зелёным клетку.
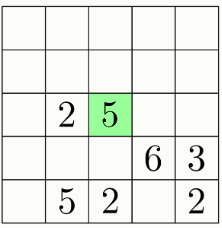
Задание 5. На физкультуре Аля, Беня, Веня, Геша и Дуся встали в одну колонну, причём некоторые встали лицом вперёд, а некоторые — лицом назад. Человек видит всех людей перед собой в колонне в направлении его взгляда. Известно, что: Алю никто не видит; Геша не видит Дусю, но видит Беню; Дуся видит Гешу, но не видит Веню; Беня не видит никого; Веня стоит раньше Бени, но не видит его. Определите порядок, в котором стоят дети.
Задание 5.1 На физкультуре Аля, Беня, Веня, Геша и Дуся встали в одну колонну, причём некоторые встали лицом вперёд, а некоторые — лицом назад. Человек видит всех людей перед собой в колонне в направлении его взгляда. Известно, что: Дусю никто не видит; Беня не видит Гешу, но видит Веню; Геша видит Беню, но не видит Алю; Веня не видит никого; Аля стоит раньше Вени, но не видит его. Определите порядок, в котором стоят дети.
Задание 6. Вася задумал три вещественных числа a, b, c. Оказалось, что три прямые, заданные уравнениями y=ax+1𝑦, y=bx+6 и y=cx+1, пересекаются в одной точке. Найдите значение b, если известно, что a+c=73.
Задание 6.1 Вася задумал три вещественных числа а, b, с. Оказалось, что три прямые, заданные уравнениями у = ах + 5, y = bx + 7 и у сx + 9, пересекаются в одной точке. Найдите значение в, если известно, что а + c = 39.
Задание 6.2 Вася задумал три вещественных числа а, b, с. Оказалось, что три прямые, заданные уравнениями у — а + 3, y= x + 7 и у = с + 11, пересекаются в одной точке. Найдите значение в, если известно, что а + c = 51.
Задание 6.3 Вася задумал три вещественных числа а, b, с. Оказалось, что три прямые, заданные уравнениями у — аx + 2, y= x + 5 и у = с + 8, пересекаются в одной точке. Найдите значение b, если известно, что а + с = 67.
Задание 7. Дан прямоугольный треугольник ABC с прямым углом A. На плоскости нашлась точка X, для которой AB=BX и AX=XC. Чему может быть равен угол BAX, если угол BXCBXC равен 138∘? Ответ выразите в градусах. Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости
Задание 7.1 Дан прямоугольный треугольник АВС с прямым углом А. На плоскости нашлась точка Х, для которой АВ — ВХ и АХ = ХС. Чему может быть равен угол ВАХ, если угол ВХС равен 117? Ответ выразите в градусах. Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
Задание 7.2 Дан прямоугольный треугольник АВС с прямым углом А. На плоскости нашлась точка Х для которой АВ — ВХ и АХ — ХС. Чему может быть равен угол ВАХ, если угол ВХС равен 108? Ответ выразите в градусах. Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
Задание 7.3 Дан прямоугольный треугольник АВС с прямым углом А. На плоскости нашлась точка Х, для которой АВ — ВХ и АХ = ХС. Чему может быть равен угол ВАХ, если угол ВХС равен 123°? Ответ выразите в градусах. Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
Задание 8. В турнире онлайн-игры участвуют 256 персонажей. В каждом из 8 раундов персонажи разбиваются на пары, сражаются между собой, победитель проходит дальше.
Изначально уровни персонажей были равны 1, 2, ……, 256. В битве всегда побеждает персонаж с бо́льшим уровнем, а если уровни одинаковы, может победить любой. После каждого тура уровень персонажа может измениться на 1 в ту или иную сторону, а может остаться прежним.
Задание 8.1 В турнире онлайн-игры участвуют 64 персонажа. В каждом из 6 раундов персонажи разбиваются на пары, сражаются между собой, победитель проходит дальше. Изначально уровни персонажей были равны 1, 2,…, 64. В битве всегда побеждает персонаж с большим уровнем, а если уровни одинаковы, может победить любой. После каждого тура уровень персонажа может измениться на 1 в ту или иную сторону, а может остаться прежним.
Задание 8.2 В турнире онлайн-игры участвуют 512 персонажей. В каждом из 9 раундов персонажи разбиваются на пары, сражаются между собой, победитель проходит дальше. Изначально уровни персонажей были равны 1, 2, …, 512. В битве всегда побеждает персонаж с большим уровнем, а если уровни одинаковы, может победить любой. После каждого тура уровень персонажа может измениться на 1 в ту или иную сторону, а может остаться прежним.
Задание 8.3 В турнире онлайн-игры участвуют 128 персонажей. В каждом из 7 раундов персонажи разбиваются на пары, сражаются между собой, победитель проходит дальше. Изначально уровни персонажей были равны 1, 2, …, 128. В битве всегда побеждает персонаж с большим уровнем, а если уровни одинаковы, может победить любой. После каждого тура уровень персонажа может измениться на 1 в ту или иную сторону, а может остаться прежним.
Персонаж с каким наименьшим стартовым уровнем мог победить в турнире?
9 класс
Задание 1. Есть 90 литров смеси, в которой доли красной, зелёной и синей красок равняются 35%, 25% и 40% соответственно. Сколько литров красной и зелёной краски нужно добавить, чтобы получилась смесь с 40% красной, 30% зелёной и 30% синей красок? Синюю краску добавлять нельзя.
Красной: л
Зелёной: л
Задание 1.1 Есть 70 литров смеси, в которой доли красной, зелёной и синей красок равняются 20%, 35% и 45 % соответственно. Сколько литров красной и зелёной краски нужно добавить, чтобы получилась смесь с 25% красной, 40% зелёной и 35% синей красок? Синюю краску добавлять нельзя.
Задание 1.2 Есть 90 литров смеси, в которой доли красной, зелёной и синей красок равняются 25%, 20% и 55 % соответственно. Сколько литров красной и зелёной краски нужно добавить, чтобы получилась смесь с 30% красной, 25% зелёной и 45% синей красок? Синюю краску добавлять нельзя.
Задание 1.3 Есть 30 литров смеси, в которой доли красной, зелёной и синей красок равняются 35%, 40% и 25% соответственно. Сколько литров красной и зелёной краски нужно добавить, чтобы получилась смесь с 40% красной, 45% зелёной и 15% синей красок? Синюю краску добавлять нельзя.
Задание 2. В таблице 6×6 отметили несколько клеток. После этого слева от каждой строки написали, сколько клеток от левой границы до первой отмеченной клетки в этой строке свободны. Аналогичные числа записали сверху, справа и снизу. После этого числа сверху, а также отметки в клетках стёрли.
Найдите количество отмеченных клеток. Восстановите числа, которые были записаны сверху.
Задание 3. Два равносторонних треугольника с параллельными сторонами расположены так, как показано на рисунке. Оказалось, что расстояния между параллельными сторонами треугольников равны 3√3. Найдите разность периметров этих треугольников.
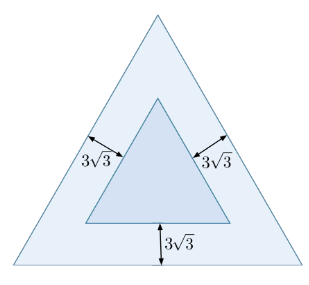
Задание 4. Числа 3, 6, 11, 16, 23 и 31 разбили на три группы по два числа так, что выполняются следующие условия:в первой группе оказались только простые числа,во второй группе сумма чисел делится на 3,сумма чисел в третьей группе больше половины от общей суммы.
Какие числа в какой группе?
3
6
11
16
23
31
Первая группа
Вторая группа
Третья группа
Задание 4.1 Числа 2, 6, 11, 15, 23 и 31 разбили на три группы по два числа так, что выполняются следующие условия: в первой группе оказались только простые числа, во второй группе сумма чисел делится на 3, сумма чисел в третьей группе больше половины от общей суммы. Какие числа в какой группе?
Задание 4.2 Числа 3, 8, 11, 17, 22 и 31 разбили на три группы по два числа так, что выполняются следующие условия: в первой группе оказались только простые числа, во второй группе сумма чисел делится на 3, сумма чисел в третьей группе больше половины от общей суммы. Какие числа в какой группе?
Задание 4.3 Числа 2, 6, 11, 15, 23 и 31 разбили на три группы по два числа так, что выполняются следующие условия: в первой группе оказались только простые числа, во второй группе сумма чисел делится на 3, сумма чисел в третьей группе больше половины от общей суммы. Какие числа в какой группе?
Задание 5. Дан треугольник АВС с прямым углом С. Окружность с центром в А, проходящая через С, пересекает гипотенузу в точке Е, а окружность с центром в В, проходящая через С, пересекает гипотенузу в точке Д. Найдите ED, если AD = 15, BE = 30.
Задание 5.1 Дан треугольник АВС с прямым углом С. Окружность с центром в А, проходящая через С, пересекает гипотенузу в точке Е, а окружность с центром в В, проходящая через С, пересекает гипотенузу в точке Д. Найдите ED, если AD = 12, BE = 54.
Задание 5.2 Дан треугольник АВС с прямым углом С. Окружность с центром в А, проходящая через С, пересекает гипотенузу в точке Е, а окружность с центром в В, проходящая через С, пересекает гипотенузу в точке Д. Найдите ED, если AD = 16, BE = 50.
Задание 5.3 ан треугольник АВС с прямым углом С. Окружность с центром в А, проходящая через С, пересекает гипотенузу в точке Е, а окружность с центром в В, проходящая через С, пересекает гипотенузу в точке Д. Найдите ED, если AD = 14, BE = 112.
Задание 6. В квадрате 5×5 расставили натуральные числа от 1 до 25, каждое по одному разу, так, что суммы чисел в каждой строке, каждом столбце и каждой из двух диагоналей совпали. Оказалось, что в центре стоит число 18. Чему может быть равна сумма чисел в отмеченных клетках?

Задание 6.1 В квадрате 5×5 расставили натуральные числа от 1 до 25, каждое по одному разу, так, что суммы чисел в каждой строке, каждом столбце и каждой из двух диагоналей совпали. Оказалось, что в центре стоит число 17. Чему может быть равна сумма чисел в отмеченных клетках?

Задание 6. В квадрате 5×5 расставили натуральные числа от 1 до 25, каждое по одному разу, так, что суммы чисел в каждой строке, каждом столбце и каждой из двух диагоналей совпали. Оказалось, что в центре стоит число 17. Чему может быть равна сумма чисел в отмеченных клетках?
Задание 6. В квадрате 5×5 расставили натуральные числа от 1 до 25, каждое по одному разу, так, что суммы чисел в каждой строке, каждом столбце и каждой из двух диагоналей совпали. Оказалось, что в центре стоит число 9. Чему может быть равна сумма чисел в отмеченных клетках?
Задание 6. В квадрате 5×5 расставили натуральные числа от 1 до 25, каждое по одному разу, так, что суммы чисел в каждой строке, каждом столбце и каждой из двух диагоналей совпали. Оказалось, что в центре стоит число 9. Чему может быть равна сумма чисел в отмеченных клетках?
Задание 7. Натуральные числа а, в таковы, что число 9a+10b/a+2b тоже натуральное. Чему может быть a+2b a равно отношение a\b? Укажите все подходящие варианты. Каждый ответ записывайте b в отдельное поле, добавляя их при необходимости.
Задание 8. На квалификационное соревнование, по результатам которого отбираются участники на областной чемпионат, подали заявки 80 команд. Отбор происходит по следующей схеме. У каждой команды есть некоторый счёт побед и поражений (изначально 0-0). В каждом матче принимают участие две команды с одинаковым текущим счётом, и одна из них побеждает, а другая проигрывает (ничьих не бывает). Если команда набирает 3 поражения, она выбывает из отбора. Если команда набирает 3 победы, она выходит в основную часть тоже прекращает участие в квалификационном соревновании. Турнир оканчивается, И когда судьба каждой команды будет определена. Сколько команд попадёт на областной чемпионат? Сколько будет сыграно матчей?
Задание 8.1 На квалификационное соревнование, по результатам которого отбираются участники на областной чемпионат, подали заявки 112 команд. Отбор происходит по следующей схеме. У каждой команды есть некоторый счёт побед и поражений (изначально 0-0). В каждом матче принимают участие две команды с одинаковым текущим счётом, и одна из них побеждает, а другая проигрывает (ничьих не бывает). Если команда набирает 3 поражения, она выбывает из отбора. Если команда набирает 3 победы, она выходит в основную часть И тоже прекращает участие в квалификационном соревновании. Турнир оканчивается, когда судьба каждой команды будет определена. Сколько команд попадёт на областной чемпионат? Сколько будет сыграно матчей?
Задание 8.2 На квалификационное соревнование, по результатам которого отбираются участники областной чемпионат, подали заявки 96 команд. Отбор происходит по следующей схеме. У каждой команды есть некоторый счёт побед и поражений (изначально 0-0). В каждом матче принимают участие две команды с одинаковым текущим счётом, и одна из них побеждает, а другая проигрывает (ничьих не бывает). Если команда набирает 3 поражения, она выбывает из отбора. Если команда набирает 3 победы, она выходит в основную часть тоже прекращает участие в квалификационном соревновании. Турнир оканчивается, когда судьба каждой команды будет определена. И Сколько команд попадёт на областной чемпионат? Сколько будет сыграно матчей?
Задание 8.3 На квалификационное соревнование, по результатам которого отбираются участники на областной чемпионат, подали заявки 128 команд. Отбор происходит по следующей схеме. У каждой команды есть некоторый счёт побед и поражений (изначально 0-0). В каждом матче принимают участие две команды с одинаковым текущим счётом, и одна из них побеждает, а другая проигрывает (ничьих не бывает). Если команда набирает 3 поражения, она выбывает из отбора. Если команда набирает 3 победы, она выходит в основную часть и тоже прекращает участие в квалификационном соревновании. Турнир оканчивается, когда судьба каждой команды будет определена. Сколько команд попадёт на областной чемпионат?
10 класс
Задание 1. Найдите максимальное натуральное число n>100— такое, что при стирании двух последних цифр оно уменьшается ровно в 115 раз.
Задание 1.2 Найдите максимальное натуральное число n>100— такое, что при стирании двух последних цифр оно уменьшается ровно в 113 раз.
Задание 1.3 Найдите максимальное натуральное число n>100— такое, что при стирании двух последних цифр оно уменьшается ровно в 112 раз.
Задание 1.4 Найдите максимальное натуральное число n>100— такое, что при стирании двух последних цифр оно уменьшается ровно в 114 раз.
→ Получить ответы
Задание 2. В конкурсе участвовало несколько танцевальных пар. Каждый пожал руку всем остальным, кроме себя и своего партнёра. Всего было сделано 80400 рукопожатий. Сколько было пар?
Задание 2.1 В конкурсе участвовало несколько танцевальных пар. Каждый пожал руку всем остальным, кроме себя и своего партнёра. Всего было сделано 20200 рукопожатий. Сколько было пар?
→ Получить ответы
Задание 3. Последовательность целых чисел {xn} такова, что x1=1300 и xn+1=∣xn−7∣ для всех n>1 Найдите такое минимальное n, что xn+2=xn.
Задание 3.1 Последовательность целых чисел {xn} такова, что x1=1000 и xn+1=∣xn−7∣ для всех n>1 Найдите такое минимальное n, что xn+2=xn.
→ Получить ответы
Задание 4. На праздновании Нового года 46 школьников встали в хоровод. Каждую минуту один из школьников, которому не дарили подарков и который не дарил подарок, дарит подарок одному из двух ближайших слева соседей. Можно дарить подарок школьнику, у которого уже есть подарок. Когда каждый школьник подарил или получил хотя бы один подарок, обмен подарками заканчивается.
Задание 4.1 На праздновании Нового года 43 школьников встали в хоровод. Каждую минуту один из школьников, которому не дарили подарков и который не дарил подарок, дарит подарок одному из двух ближайших слева соседей. Можно дарить подарок школьнику, у которого уже есть подарок. Когда каждый школьник подарил или получил хотя бы один подарок, обмен подарками заканчивается.
Задание 4.2 На праздновании Нового года 40 школьников встали в хоровод. Каждую минуту один из школьников, которому не дарили подарков и который не дарил подарок, дарит подарок одному из двух ближайших слева соседей. Можно дарить подарок школьнику, у которого уже есть подарок. Когда каждый школьник подарил или получил хотя бы один подарок, обмен подарками заканчивается.
Какое максимальное количество школьников могло получить подарки?
Какое минимальное количество школьников могло получить подарки?
→ Получить ответы
Задание 5. В описанном четырёхугольнике ABCD оказалось, что ABC = ACD = 90°, AB = 7, BC =5. Найдите CD.
Задание 5.1 В описанном четырёхугольнике ABCD оказалось, что ABC = ACD = 90°, AB = 5, BC = 3. Найдите CD.
→ Получить ответы
Задание 6. Каждый член последовательности натуральных чисел, начиная с третьего, равен сумме двух предыдущих, а восьмой член равен 2613. Сколько существует таких последовательностей? Чему равен второй член последовательности, если первый равен 13?
Задание 6.1 Каждый член последовательности натуральных чисел, начиная с третьего, равен сумме двух предыдущих, а восьмой член равен 3900. Сколько существует таких последовательностей? Чему равен второй член последовательности, если первый равен 13?
Задание 6.2 Каждый член последовательности натуральных чисел, начиная с третьего, равен сумме двух предыдущих, а восьмой член равен 650. Сколько существует таких последовательностей? Чему равен второй член последовательности, если первый равен 13?
Задание 6.3 Каждый член последовательности натуральных чисел, начиная с третьего, равен сумме двух предыдущих, а восьмой член равен 1313. Сколько существует таких последовательностей? Чему равен второй член последовательности, если первый равен 13?
Задание 1.2 Найдите максимальное натуральное число n>100— такое, что при стирании двух последних цифр оно уменьшается ровно в 113 раз.
Задание 1.3 Найдите максимальное натуральное число n>100— такое, что при стирании двух последних цифр оно уменьшается ровно в 112 раз.
Задание 1.4 Найдите максимальное натуральное число n>100— такое, что при стирании двух последних цифр оно уменьшается ровно в 114 раз.
→ Получить ответы
Задание 2. В конкурсе участвовало несколько танцевальных пар. Каждый пожал руку всем остальным, кроме себя и своего партнёра. Всего было сделано 80400 рукопожатий. Сколько было пар?
Задание 2.1 В конкурсе участвовало несколько танцевальных пар. Каждый пожал руку всем остальным, кроме себя и своего партнёра. Всего было сделано 20200 рукопожатий. Сколько было пар?
→ Получить ответы
Задание 3. Последовательность целых чисел {xn} такова, что x1=1300 и xn+1=∣xn−7∣ для всех n>1 Найдите такое минимальное n, что xn+2=xn.
Задание 3.1 Последовательность целых чисел {xn} такова, что x1=1000 и xn+1=∣xn−7∣ для всех n>1 Найдите такое минимальное n, что xn+2=xn.
→ Получить ответы
Задание 4. На праздновании Нового года 46 школьников встали в хоровод. Каждую минуту один из школьников, которому не дарили подарков и который не дарил подарок, дарит подарок одному из двух ближайших слева соседей. Можно дарить подарок школьнику, у которого уже есть подарок. Когда каждый школьник подарил или получил хотя бы один подарок, обмен подарками заканчивается.
Задание 4.1 На праздновании Нового года 43 школьников встали в хоровод. Каждую минуту один из школьников, которому не дарили подарков и который не дарил подарок, дарит подарок одному из двух ближайших слева соседей. Можно дарить подарок школьнику, у которого уже есть подарок. Когда каждый школьник подарил или получил хотя бы один подарок, обмен подарками заканчивается.
Задание 4.2 На праздновании Нового года 40 школьников встали в хоровод. Каждую минуту один из школьников, которому не дарили подарков и который не дарил подарок, дарит подарок одному из двух ближайших слева соседей. Можно дарить подарок школьнику, у которого уже есть подарок. Когда каждый школьник подарил или получил хотя бы один подарок, обмен подарками заканчивается.
Какое максимальное количество школьников могло получить подарки?
Какое минимальное количество школьников могло получить подарки?
→ Получить ответы
Задание 5. В описанном четырёхугольнике ABCD оказалось, что ABC = ACD = 90°, AB = 7, BC =5. Найдите CD.
Задание 5.1 В описанном четырёхугольнике ABCD оказалось, что ABC = ACD = 90°, AB = 5, BC = 3. Найдите CD.
→ Получить ответы
Задание 6. Каждый член последовательности натуральных чисел, начиная с третьего, равен сумме двух предыдущих, а восьмой член равен 2613. Сколько существует таких последовательностей? Чему равен второй член последовательности, если первый равен 13?
Задание 6.1 Каждый член последовательности натуральных чисел, начиная с третьего, равен сумме двух предыдущих, а восьмой член равен 3900. Сколько существует таких последовательностей? Чему равен второй член последовательности, если первый равен 13?
Задание 6.2 Каждый член последовательности натуральных чисел, начиная с третьего, равен сумме двух предыдущих, а восьмой член равен 650. Сколько существует таких последовательностей? Чему равен второй член последовательности, если первый равен 13?
Задание 6.3 Каждый член последовательности натуральных чисел, начиная с третьего, равен сумме двух предыдущих, а восьмой член равен 1313. Сколько существует таких последовательностей? Чему равен второй член последовательности, если первый равен 13?
11 класс
Задание 1. Дана арифметическая прогрессия {an}, такая, что a1+a2=11, a1+a2+a3+…+a8=164.
→ Получить ответы
Задание 2. У Вити есть четыре карточки, на которых написаны числа 1, 2, 4, 7. Он случайным образом составляет из них число вида ab¯¯¯¯¯cd¯. С какой вероятностью это число делится на 3?
Выражение ab¯¯¯¯¯ обозначает двухзначное число, состоящее из цифр a и b.
→ Получить ответы
Задание 3. Во вписанном четырёхугольнике ABCD отметили точку E пересечение лучей AD и BC и точку F пересечение лучей AB и DC. Оказалось, что CD=DE, ∠AEB=51∘ и угловые меры дуг BC и AD находятся в соотношении 2:5 Найдите угол AFD. Ответ выразите в градусах.
→ Получить ответы
Задание 4. Найдите количество пар различных натуральных чисел a, b, таких, что 1⩽a<b⩽100 и ⌊a√⌋+⌈b√⌉=⌈a√ ⌉+⌊b√⌋. Напомним, что ⌊x⌋обозначает наибольшее целое число, меньшее или равное x𝑥, а ⌈x⌉ наименьшее целое число, большее или равное x.
→ Получить ответы
Задание 5. Дана колода из 300 карт, на каждой из которых записано натуральное число от 1 до 300 (каждое число встречается по одному разу). Петя раскладывает пасьянс. Для этого Петя выкладывает карты в прямоугольник 3×100 (3 строки, 100 столбцов) так, что числа на картах в каждом столбце возрастают сверху вниз, а также любое число в нижней строке больше любого числа в верхней строке. Удачностью пасьянса называется сумма всех чисел на карточках в верхней и нижней строках. Какой максимальной удачности пасьянс может выложить Петя?
→ Получить ответы
Задание 6. Толя задумал два квадратных трёхчлена. Корни первого трёхчлена равны 1 и 2, а один из двух корней второго трёхчлена равен −5. Также известно, что графики трёхчленов пересекаются в двух точках: одна из них имеет координаты (3, 4), а вторая лежит на оси ординат.
Найдите ординату второй точки пересечения графиков.
Найдите произведение корней второго трёхчлена.
→ Получить ответы
Задание 2. У Вити есть четыре карточки, на которых написаны числа 1, 2, 4, 7. Он случайным образом составляет из них число вида ab¯¯¯¯¯cd¯. С какой вероятностью это число делится на 3?
Выражение ab¯¯¯¯¯ обозначает двухзначное число, состоящее из цифр a и b.
→ Получить ответы
Задание 3. Во вписанном четырёхугольнике ABCD отметили точку E пересечение лучей AD и BC и точку F пересечение лучей AB и DC. Оказалось, что CD=DE, ∠AEB=51∘ и угловые меры дуг BC и AD находятся в соотношении 2:5 Найдите угол AFD. Ответ выразите в градусах.
→ Получить ответы
Задание 4. Найдите количество пар различных натуральных чисел a, b, таких, что 1⩽a<b⩽100 и ⌊a√⌋+⌈b√⌉=⌈a√ ⌉+⌊b√⌋. Напомним, что ⌊x⌋обозначает наибольшее целое число, меньшее или равное x𝑥, а ⌈x⌉ наименьшее целое число, большее или равное x.
→ Получить ответы
Задание 5. Дана колода из 300 карт, на каждой из которых записано натуральное число от 1 до 300 (каждое число встречается по одному разу). Петя раскладывает пасьянс. Для этого Петя выкладывает карты в прямоугольник 3×100 (3 строки, 100 столбцов) так, что числа на картах в каждом столбце возрастают сверху вниз, а также любое число в нижней строке больше любого числа в верхней строке. Удачностью пасьянса называется сумма всех чисел на карточках в верхней и нижней строках. Какой максимальной удачности пасьянс может выложить Петя?
→ Получить ответы
Задание 6. Толя задумал два квадратных трёхчлена. Корни первого трёхчлена равны 1 и 2, а один из двух корней второго трёхчлена равен −5. Также известно, что графики трёхчленов пересекаются в двух точках: одна из них имеет координаты (3, 4), а вторая лежит на оси ординат.
Найдите ординату второй точки пересечения графиков.
Найдите произведение корней второго трёхчлена.
Часть ответов по ВсОШ публикуется бесплатно в нашем Telegram-канале: @shcolaotvet