15.10.2025 — ВСОШ СИРИУС Школьный этап по Математике 4-6 класс: задания и ответы для 2 группы
Авторские решения к этой работе доступны для покупки на нашем сайте:
Группа №2 включает регионы: Белгородская область (31), Брянская область (32), Владимирская область (33), Воронежская область (36), город Санкт-Петербург (78), Ивановская область (37), Калининградская область (39), Калужская область (40), Кировская область (43), Костромская область (44), Курская область (46), Ленинградская область (47), Липецкая область (48), Нижегородская область (52), Орловская область (57), Республика Марий Эл (12), Республика Мордовия (13), Республика Татарстан (16), Республика Чувашия (21), Рязанская область (62), Смоленская область (67), Тамбовская область (68), Тверская область (69), Тульская область (71), Ярославская область (76).
Рассмотрим задания и ответы по Математике для 4–6 классов:
Навигация
4 класс
Задание 1. Дети играют в игру. За один ход можно стереть последнюю цифру написанного на доске числа или записать вместо него вдвое большее число. Запишите последовательность из четырёх ходов, которая позволит из 56 получить 40.
Задание 2. По кольцевому маршруту ездят 5 автобусов с одинаковой скоростью, причём интервал движения составляет 30 минут, т. е. в любое место на маршруте каждый следующий автобус прибывает через 30 минут после предыдущего. Со следующей недели на маршрут добавят ещё один автобус, который будет двигаться с той же скоростью, и поменяют расписание так, чтобы и теперь промежуток времени между автобусами был постоянный. Какой интервал движения будет на следующей неделе? Ответ выразите в минутах.
Задание 3. В каждой клетке таблицы 3×3 стоят нули. Над таблицей можно проводить следующие операции: прибавить 1 к каждому из чисел, написанных в ячейках любой строки, прибавить 2 к каждому из чисел, написанных в ячейках любого столбца. В некотором порядке a раз провели первую операцию и b раз вторую. Получили следующую таблицу.
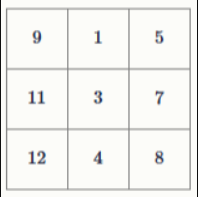
Задание 4. На столе лежат 10 монет достоинством 5 и 10 рублей. Семь детей взяли монеты, и ни одной не осталось. Каждый брал одну монету или две, но разного достоинства. У Антона оказалось меньше рублей, чем у любого из остальных детей. Какая сумма денег лежала на столе? Ответ выразите в рублях.
Задание 5. Даны 19 квадратов со сторонами 1 , 2 , … … , 19 . Они выстроены вдоль одной прямой в виде лестницы, как показано на примере.
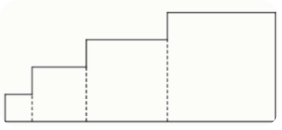
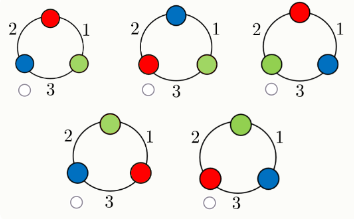
Задание 6. Аня, Валя и Оля после уроков вспоминали, как они провели лето. В июне в торговом центре они встретили промоутера, который раздавал бумажные цветы. В этот момент у него осталось пять цветков, показанных на рисунке.Каждой девочке он дал по одному цветку.
Валя сказала: «Я помню, какого цвета цветок я получила, но не помню, какой формы».
Чуть позже она добавила: «Я также помню, какого цвета цветок подарили Оле, но не помню, какой формы». Аня сказала: «А я помню, какой формы цветок я получила, но не помню, какого цвета».
После этого Валя поняла, какой цветок достался Ане. Какой?

Сувениры какого цвета получили Валя и Оля?
- Валя
- Оля
- Фиолетовый
- Оранжевый
Задание 7. Из одинаковых кубиков сложили конструкцию. На рисунке представлен её вид спереди, сверху и слева.
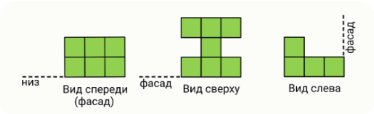
Из скольких кубиков состоит конструкция?
Задание 8. 90 камней разложили на 5 кучек так, что во всех кучках оказалось разное число камней, не равное нулю. В кучке Ромы оказалось больше всего камней. Какое наибольшее число камней может быть в кучке Ромы? Число Какое наименьшее число камней может быть в кучке Ромы?
5 класс
Задание 1. Петя и Вася выбежали утром на пробежку по дорожкам парка, которые разбивают его на 25 одинаковых квадратных секторов. Схема парка представлена справа. Оба начали тренировку в точке A и закончили в этой же точке. Петин маршрут показан красным цветом, а Васин синим. Каждый из них пробегал сторону одного сектора (сторону квадрата) за 1 минуту. Сколько минут Петя и Вася бежали вместе бок о бок?
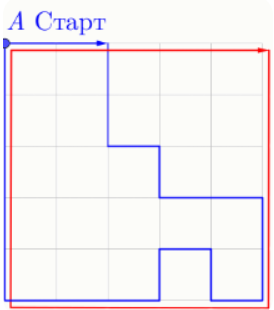
- 2 минуты
- 5 минут
- 6 минут
- 13 минут
- 25 минут
- Нет верного ответа
Задание 2. На стол бросили пять игральных кубиков. Они упали так, как показано на рисунке. На каждую грань кубика нанесены от 1 до 6 точек. Можно несколько раз проделать следующую операцию: выбрать любой кубик и перевернуть его произвольным образом так, чтобы чётность числа на верхней грани не изменилась. Какую сумму чисел на верхних гранях можно получить? Выберите все подходящие варианты:

Задание 3. По кругу расположены 3 цветных шарика, как показано на рисунке: зелёный, синий и красный.
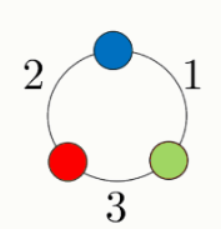
Далее выполняются следующие действия: первым ходом меняются местами шарики, соединённые дугой 1 , вторым ходом соединённые дугой 2 , третьим ходом соединённые дугой 3 , четвёртым ходом снова шарики, соединённые дугой 1 , и т. д. Как будут расположены шарики после 45 ходов?
Задание 4. В очереди в школьной столовой стоят Максим и Даниил. Перед Максимом стоят 7 человек, а после Даниила 12 . Сколько человек может быть в очереди, если между Максимом и Даниилом 5 человек? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
Задание 5. У Маши есть 8 8 карточек с цифрами 4 , 6 , 8 , 1 , 3 , 5 , 7 , 9 и пример на вычисление. В каждую ячейку нужно поставить ровно одну карточку и выполнить действия с тремя полученными числами. Какой максимальный результат можно получить?
Задание 6. У Пети есть два одинаковых треугольника со сторонами 3, 4, 6 сантиметров. Он составляет из них фигуру, прикладывая один треугольник к другому без наложений.
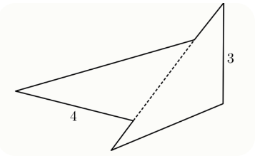
Найдите периметр фигуры, изображённой на рисунке. Ответ выразите в сантиметрах.
Какой наименьший периметр может иметь фигура, составленная таким образом? Ответ выразите в сантиметрах.
Задание 7. Перед концертом Петя и Вася расставили стулья в актовом зале в форме прямоугольника. Петя выбрал для себя шестое место в шестом ряду. После этого пришла учительница, забрала с одного края из каждого ряда некоторое одинаковое количество стульев и переставила их вперёд так, что снова образовался прямоугольник. В результате Петино место оказалось четвёртым в восьмом ряду. Какое наименьшее количество стульев могло быть в зале?
Задание 8. Требуется раскрасить белые шары на рисунке в три цвета: красный, зелёный и синий, так чтобы никакие два шара одного цвета не были соединены линией.
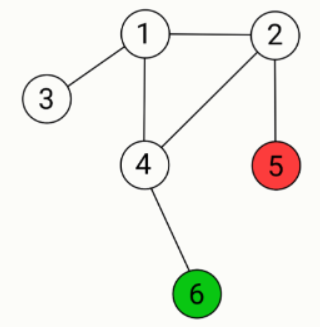
Сколькими способами можно это сделать?
6 класс
Задание 1. Из 27 кубиков размером 1×1×1 сложили куб 3×3×3. Он состоит из 11 красных и 16 синих кубиков.
Какая наименьшая площадь поверхности куба 3×3×3 может быть красной?
Какая наибольшая площадь поверхности куба 3×3×3может быть красной?
Задание 2. Даны два квадрата с целыми сторонами a и b (a<b).
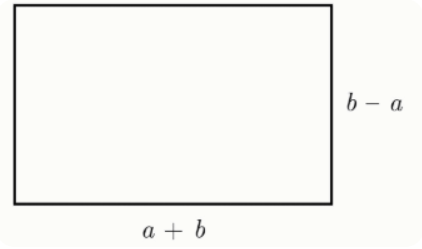
Площадь изображённого прямоугольника равна 47.
Найдите a.
Найдите b.
Задание 3. Назовём горизонталь, вертикаль или одну из двух главных диагоналей квадрата рядом. В квадрате 3×3 расставили числа так, что для любого его ряда верно, что число, расположенное в его середине, вдвое меньше суммы крайних чисел этого ряда. Из квадрата стёрли некоторые числа. Восстановите их.
Задание 4. На плоскости проведены 32 прямые, причём каждая параллельна ровно трём другим и никакие три прямые не пересекаются в одной точке. Сколько точек пересечения у этих прямых?
Задание 5. По кругу стоят 60 чередующихся стульев: чёрных и белых. На стулья сели представители двух племён: рыцари и лжецы. Рыцари всегда говорят правду, лжецы всегда лгут. Каждый сидящий на белом стуле заявил, что среди двух человек, следующих за ним по часовой стрелке, есть рыцарь. Каждый сидящий на чёрном стуле заявил, что среди двух человек, следующих за ним по часовой стрелке, нет рыцаря. Сколько рыцарей могло сидеть за столом? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
Задание 6. В каждом столбце, в каждой строке и в каждой выделенной фигуре таблицы должно быть по одной букве A, B, C, D, E. Таблицу заполнили частично.
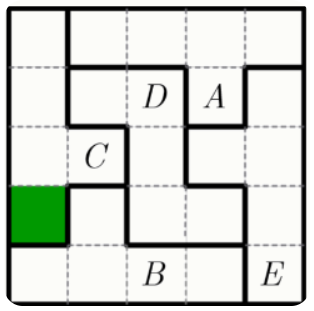
Какая буква расположена в отмеченной клетке?
Задание 7. Роботы‑рекультиваторы ликвидируют последствия разлива радиоактивного вещества, снимая верхний слой почвы с участка. Вся загрязнённая почва может быть убрана одним роботом за 42 часа. Ангар с первым роботом располагается в 1 км от участка, со вторым в 2 км и т. д. Все роботы выехали из ангаров одновременно и начинали удаление почвы, как только достигали участка. Когда последний робот добрался до участка, оказалось, что загрязнённую почву только что полностью убрали. Известно, что первый робот убрал в шесть раз больше предпоследнего. Производительность и скорость передвижения всех роботов одинакова.
Сколько часов снимал почву первый робот?
Сколько часов первый робот ехал до поля?
Задание 8. В государстве 28 городов располагаются на территории областей так, что любые два города из одной области соединены дорогой и никакие два города из разных областей дорогой не соединены. Оказалось, что ответственность за состояние дорог можно распределить между двумя региональными министерствами следующим образом: не найдётся таких трёх городов A, B, C из одной области, чтобы дороги AB , BC и CA обслуживались бы одним министерством. Какое наибольшее число дорог может быть в этом государстве?
Часть ответов по ВсОШ публикуется бесплатно в нашем Telegram-канале: @shcolaotvet